Vrijeme: 05:32
Pješke do Samobora! | Walking to Samobor! #5
Fran je prošao kroz Bestovje i ušao u Svetu Nedelju. Opasno se približava Samoboru, a također je otkrio da na mobitelu ima još jednu pjesmu Visokih pet, Jackie Chan. Zbog toga je odlučio uživati u pjesmi i smisliti zadatak kojeg će zadati Borni kad stigne do Samobora. Fran je dobar prijatelj i zapamtio je da je Borni omiljeno područje geometrija, tako da je zadnji zadatak odlučio začiniti najljepšim područjem natjecateljske matematike. Zadatak glasi ovako: U trokutu  najkraća stranica je duljine
najkraća stranica je duljine  , a duljine preostale dvije su također cijeli brojevi. Za duljine visina tog trokuta vrijedi:
, a duljine preostale dvije su također cijeli brojevi. Za duljine visina tog trokuta vrijedi: 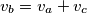 . Odredi sumu opsega svih trokuta koji zadovoljavaju uvjete zadatka. Pomognite Franu da riješi zadatak prije Borne.
. Odredi sumu opsega svih trokuta koji zadovoljavaju uvjete zadatka. Pomognite Franu da riješi zadatak prije Borne.
 najkraća stranica je duljine
najkraća stranica je duljine  , a duljine preostale dvije su također cijeli brojevi. Za duljine visina tog trokuta vrijedi:
, a duljine preostale dvije su također cijeli brojevi. Za duljine visina tog trokuta vrijedi: 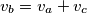 . Odredi sumu opsega svih trokuta koji zadovoljavaju uvjete zadatka. Pomognite Franu da riješi zadatak prije Borne.
. Odredi sumu opsega svih trokuta koji zadovoljavaju uvjete zadatka. Pomognite Franu da riješi zadatak prije Borne. Fran passed through Bestovje and entered Sveta Nedelja, getting closer to Samobor. He also discovered that he had another song by Visoki Pet, Jackie Chan, on his phone. Enjoying the music, Fran decided to come up with a problem to challenge Borna when he arrived in Samobor. Knowing that Borna’s favorite area is geometry, Fran decided to spice up the last task with the most beautiful part of competitive math. The problem is as follows:
In triangle 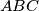 , the shortest side has a length of 5, and the lengths of the other two sides are also integers. The heights of this triangle satisfy:
, the shortest side has a length of 5, and the lengths of the other two sides are also integers. The heights of this triangle satisfy: 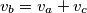 . Find the sum of the perimeters of all triangles that satisfy the conditions of the problem. Help Fran solve the problem before Borna does.
. Find the sum of the perimeters of all triangles that satisfy the conditions of the problem. Help Fran solve the problem before Borna does.
