Jednog predivnog poslijepodneva, u svojim tajnim odajama u Kaštel Štafiliću raspravljala su dva slavna filozofa: Platon i Sokrat. Osim odgovaranja na šašava pitanja o ljudskim nagonima i raznim drugim stvarima oni su voljeli filozofirati i o nekakvim minimumima i maksimumima.
Tako je Sokrat započeo:
"Svako polje 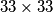 kvadratne ploče obojeno je u jedno od 3 boje: crvena, žuta ili plava, tako da ima jednako polja u svakoj od 3 boje."
kvadratne ploče obojeno je u jedno od 3 boje: crvena, žuta ili plava, tako da ima jednako polja u svakoj od 3 boje."
"Zanimljivo", na to će Platon, "daj mi pliz dodaj sapun".
Sokrat kao da ga nije ni čuo nastavlja sa svojim pitanjem:
"Ako dva polja ploče koji su različite boje dijele neku stranicu, zovemo tu stranicu Dubrovačkom. Koliko najmanje može biti Dubrovačkih stanica na našoj ploči?"
Nakon kratkog razmišljanja Platon je shvatio da zna odgovor. Koji mu je broj na umu?
One beautiful afternoon, in their secret chambers in Kaštel Štafilić, two famous philosophers, Plato and Socrates, were deep in discussion. Besides answering quirky questions about human impulses and various other things, they loved to philosophize about certain minimums and maximums.
Socrates began:
"Each square of a 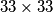 grid is colored in one of three colors: red, yellow, or blue, so that there are an equal number of squares in each of the three colors."
grid is colored in one of three colors: red, yellow, or blue, so that there are an equal number of squares in each of the three colors."
"Interesting," Plato responded, "pass me the soap, please."
Socrates, as if he hadn't heard, continued with his question:
"If two squares on the grid that are different colors share an edge, we call that edge a Dubrovnik edge. What is the minimum number of Dubrovnik edges on our grid?"
After a brief moment of thought, Plato realized he knew the answer. What number came to his mind?
[lang=hr]
Jednog predivnog poslijepodneva, u svojim tajnim odajama u Kaštel Štafiliću raspravljala su dva slavna filozofa: Platon i Sokrat. Osim odgovaranja na šašava pitanja o ljudskim nagonima i raznim drugim stvarima oni su voljeli filozofirati i o nekakvim minimumima i maksimumima.
Tako je Sokrat započeo:
"Svako polje $33\times 33$ kvadratne ploče obojeno je u jedno od 3 boje: crvena, žuta ili plava, tako da ima jednako polja u svakoj od 3 boje."
"Zanimljivo", na to će Platon, "daj mi pliz dodaj sapun".
Sokrat kao da ga nije ni čuo nastavlja sa svojim pitanjem:
"Ako dva polja ploče koji su različite boje dijele neku stranicu, zovemo tu stranicu Dubrovačkom. Koliko najmanje može biti Dubrovačkih stanica na našoj ploči?"
Nakon kratkog razmišljanja Platon je shvatio da zna odgovor. Koji mu je broj na umu?
[/lang]
[lang=en]
One beautiful afternoon, in their secret chambers in Kaštel Štafilić, two famous philosophers, Plato and Socrates, were deep in discussion. Besides answering quirky questions about human impulses and various other things, they loved to philosophize about certain minimums and maximums.
Socrates began:
"Each square of a $33\times 33$ grid is colored in one of three colors: red, yellow, or blue, so that there are an equal number of squares in each of the three colors."
"Interesting," Plato responded, "pass me the soap, please."
Socrates, as if he hadn't heard, continued with his question:
"If two squares on the grid that are different colors share an edge, we call that edge a Dubrovnik edge. What is the minimum number of Dubrovnik edges on our grid?"
After a brief moment of thought, Plato realized he knew the answer. What number came to his mind?
[/lang]
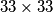 kvadratne ploče obojeno je u jedno od 3 boje: crvena, žuta ili plava, tako da ima jednako polja u svakoj od 3 boje."
kvadratne ploče obojeno je u jedno od 3 boje: crvena, žuta ili plava, tako da ima jednako polja u svakoj od 3 boje."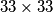 grid is colored in one of three colors: red, yellow, or blue, so that there are an equal number of squares in each of the three colors."
grid is colored in one of three colors: red, yellow, or blue, so that there are an equal number of squares in each of the three colors."