Vrijeme: 09:09
Fraktali | Fractals #3
Barbara crta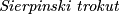 
. U prvom potezu nacrta početni trokut pa ga u drugom srednjicama podijeli na 4 manja trokuta, a u trećem sva tri manja trokuta (sve osim srednjeg) također podijeli srednjicama te tako nastavlja u beskonačnost. Ako je nakon prvog poteza na slici 1 trokut, nakon drugog 5 (četiri mala i jedan veliki), a nakon trećeg 17, koliko će trokuta biti na slici nakon 
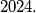poteza? Odgovor napišite modulo 
.
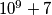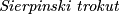. U prvom potezu nacrta početni trokut pa ga u drugom srednjicama podijeli na 4 manja trokuta, a u trećem sva tri manja trokuta (sve osim srednjeg) također podijeli srednjicama te tako nastavlja u beskonačnost. Ako je nakon prvog poteza na slici 1 trokut, nakon drugog 5 (četiri mala i jedan veliki), a nakon trećeg 17, koliko će trokuta biti na slici nakon 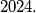poteza? Odgovor napišite modulo 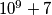. Barbara is drawing a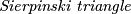 
. In the first step, she draws an initial triangle. In the second step, she divides it into four smaller triangles by connecting the midpoints of the sides. In the third step, she divides the three outer triangles (everything except the central triangle) into smaller triangles by connecting their midpoints, and she continues this process infinitely. If there is 1 triangle in the first step, 5 triangles after the second step (four smaller ones and one large one), and 17 triangles after the third step, how many triangles will there be after the 
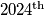step? Provide your answer modulo .
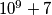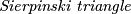. In the first step, she draws an initial triangle. In the second step, she divides it into four smaller triangles by connecting the midpoints of the sides. In the third step, she divides the three outer triangles (everything except the central triangle) into smaller triangles by connecting their midpoints, and she continues this process infinitely. If there is 1 triangle in the first step, 5 triangles after the second step (four smaller ones and one large one), and 17 triangles after the third step, how many triangles will there be after the 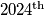step? Provide your answer modulo .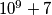