Ako je
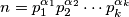
definiramo funkciju
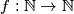
kao
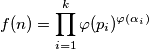
Odredi 
If
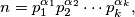
we define a function

as
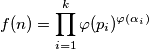
Determine 
[lang=hr]
Ako je $n = p_1^{\alpha_1} p_2^{\alpha_2} \cdots p_k ^{\alpha_k}$ definiramo funkciju $f : \mathbb N \to \mathbb N$ kao
$$f(n) = \prod_{i = 1}^{k} \varphi (p_i) ^{\varphi (\alpha_i)}$$
Odredi $$\sum_{n = 1}^{707} v_{707}(f(n!)).$$
[/lang]
[lang=en]
If
$
n = p_1^{\alpha_1} p_2^{\alpha_2} \cdots p_k^{\alpha_k},
$
we define a function $f : \mathbb{N} \to \mathbb{N}$ as
$$f(n) = \prod_{i = 1}^{k} \varphi (p_i) ^{\varphi (\alpha_i)}$$
Determine $$\sum_{n = 1}^{707} v_{707}(f(n!)).$$
[/lang]