Vrijeme: 06:38
Logično | Logical #1
U ovom lancu čemo dokazivati logičke trvdnje. Na način da čemo uvodit tvrdnje i onda ih iskorištavat. Naprimjer za dokazat nešto kao  Prvo treba pretpodstavit
Prvo treba pretpodstavit  , pa
, pa 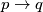 i onda na kraju ostaje dokazat
i onda na kraju ostaje dokazat  . Ove pretpostavke ćemo označiti sa
. Ove pretpostavke ćemo označiti sa  i
i  . Sada za dokazivanje
. Sada za dokazivanje  primjenit ćemo
primjenit ćemo 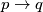 primjenit možemo jer se na desnoj strani nalazi
primjenit možemo jer se na desnoj strani nalazi  i onda ostaje dokazati
i onda ostaje dokazati  . A to nam je već jedna od pretpostavki. Primjenjivanje ćemo označiti sa negativnim predznakom npr.
. A to nam je već jedna od pretpostavki. Primjenjivanje ćemo označiti sa negativnim predznakom npr.  i
i  redom. Tako da dokaz ove trvdnje bit će niz
redom. Tako da dokaz ove trvdnje bit će niz  Dok varijable nisu bitne i nešto kao
Dok varijable nisu bitne i nešto kao 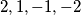 bi također trebalo biti točno. Za olakšavanje provjere zadataka sve varijable (tvrdnje) ćemo počet označavat s
bi također trebalo biti točno. Za olakšavanje provjere zadataka sve varijable (tvrdnje) ćemo počet označavat s  pa
pa  i tako nadalje po prirodnim brojevima. Da vidimo jeste li shvatili koncept dokažite trivijalnu tvrdnju
i tako nadalje po prirodnim brojevima. Da vidimo jeste li shvatili koncept dokažite trivijalnu tvrdnju 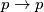 Sretno.
Sretno.
 Prvo treba pretpodstavit
Prvo treba pretpodstavit  , pa
, pa 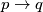 i onda na kraju ostaje dokazat
i onda na kraju ostaje dokazat  . Ove pretpostavke ćemo označiti sa
. Ove pretpostavke ćemo označiti sa  i
i  . Sada za dokazivanje
. Sada za dokazivanje  primjenit ćemo
primjenit ćemo 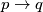 primjenit možemo jer se na desnoj strani nalazi
primjenit možemo jer se na desnoj strani nalazi  i onda ostaje dokazati
i onda ostaje dokazati  . A to nam je već jedna od pretpostavki. Primjenjivanje ćemo označiti sa negativnim predznakom npr.
. A to nam je već jedna od pretpostavki. Primjenjivanje ćemo označiti sa negativnim predznakom npr.  i
i  redom. Tako da dokaz ove trvdnje bit će niz
redom. Tako da dokaz ove trvdnje bit će niz  Dok varijable nisu bitne i nešto kao
Dok varijable nisu bitne i nešto kao 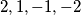 bi također trebalo biti točno. Za olakšavanje provjere zadataka sve varijable (tvrdnje) ćemo počet označavat s
bi također trebalo biti točno. Za olakšavanje provjere zadataka sve varijable (tvrdnje) ćemo počet označavat s  pa
pa  i tako nadalje po prirodnim brojevima. Da vidimo jeste li shvatili koncept dokažite trivijalnu tvrdnju
i tako nadalje po prirodnim brojevima. Da vidimo jeste li shvatili koncept dokažite trivijalnu tvrdnju 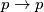 Sretno.
Sretno. In this chain we will prove logical statements. We will do it by introducing assumptions and then using them. For example, to prove something like

we first have to assume  , then
, then 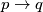 , and finally we need to prove
, and finally we need to prove  . We will label these assumptions as
. We will label these assumptions as  and
and  . Now, to prove
. Now, to prove  we apply the implication
we apply the implication 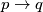 we can do this because
we can do this because  appears on the right‑hand side, and then we are left to prove
appears on the right‑hand side, and then we are left to prove  . But
. But  is already one of our assumptions. We will mark the applications with a negative sign, e.g.,
is already one of our assumptions. We will mark the applications with a negative sign, e.g.,  and
and  in order. Thus the proof of this statement will be the sequence
in order. Thus the proof of this statement will be the sequence

Any permutation of the same numbers, such as
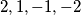
would also be correct. To make checking easier, all variables (statements) will initially be numbered 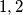 and so on, using natural numbers.
and so on, using natural numbers.
Now, to see if you have understood the concept, prove this trivial statement
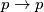
Good luck.
