Marinada '25

[lang=hr] \emph{Kraj je sve bliže i bliže, četvrti izazov ubrzo stiže!} \emph{Razmišljajući o svojim putovanjima na druge hrvatske otoke, Petar je dobio dodatnu motivaciju da izađe iz labirinta.} \emph{Kad tad ni otkuda tajanstveni glas kaže: "Riješi ovu jednadžbu za prirodne brojeve 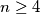$n\geq 4$."} $$\phi (n)+d(n)+n=(n-4)!-\lfloor\sqrt{n-3 }\rfloor+11$$ Riješi zajedno s Petrom ovu jednadžbu i kao odgovor na ovo pitanje zapiši zbroj kubova prethodnika svakog rješenja. Znači ako bi odgovori bili $1$ i $2$ zapisali biste $(1-1)^3+(2-1)^3$=$1$. 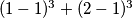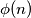$\phi(n)$ je Eulerova funkcija( Totient function). 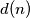$d(n)$ je funkcija koja broji djelitelje broja $n$. [/lang] [lang=en] \emph{Key to the last challnege was easily found and Peter is now going to the fourth challenge!} \emph{Reminiscing about his past voyages around the Adriatic, Peter gained extra motivation to exit this maze} \emph{Knowing all natural numbers 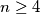$n\geq 4$, that satisfy the following relation will certainly help him:} $$\phi (n)+d(n)+n=(n-4)!-\lfloor\sqrt{n-3 }\rfloor+11$$ Help Peter solve this problem. As the answer write the sum olf the cubes of the predecessors of the numbers that satisfy the given equality. For example if the solutions were $1$ and $2$ you would write $(1-1)^3+(2-1)^3$=$1$. 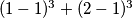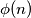$\phi(n)$ is the Euler totient function. 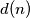$d(n)$ is the function that counts the divisors of $n$. [/lang]