After discussing some “chill” algebra problems, Ivica and Marica continue their conversation.
“I actually don’t like any algebra problem; all the other areas of mathematics are cool,” Marica proudly declared to Ivica. Upon hearing this, Ivica’s world began to fall apart, but he had a plan. He decided to give her five problems that are considered algebra, yet whose solutions are not necessarily algebraic, thereby showing her that algebra is the best field.
For the first problem, Ivica told Marica the following:
Let  be positive real numbers satisfying the following equations:
be positive real numbers satisfying the following equations:
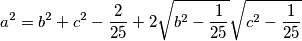
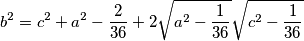
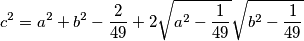
If we express 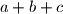 as
as 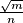 in lowest terms, what is the value of
in lowest terms, what is the value of 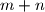 ?
?
[lang=hr]
Nakon razgovora o chill algebarskim zadatcima, Ivica i Marica nastavljaju svoj razgovor.
"Ja zapravo ne volim niti jedan zadatak iz algebre, sva ostala područja matematike su mi fora" ponosno je izjavila Marica Ivici. Na ovu rečenicu Ivici se je počeo raspadati svijet, međutim, imao je Ivica plan. Kani joj postaviti pet zadataka koji se uzimaju kao algebra, ali im rješenja nisu \textit{nužno} algebarska te time joj pokazati da je algebra najbolje područje.
Kao prvi zadatak, Ivica je Marici rekao sljedeće:
Neka $a,b,c$ budu \textbf{pozitivni} realni brojevi za koje vrijedi sljedeće:
\[
a^2=b^2+c^2-\frac{2}{25}+2\sqrt{b^2-\frac{1}{25}}\sqrt{c^2-\frac{1}{25}}
\]
\[
b^2=c^2+a^2-\frac{2}{36}+2\sqrt{a^2-\frac{1}{36}}\sqrt{c^2-\frac{1}{36}}
\]
\[
c^2=a^2+b^2-\frac{2}{49}+2\sqrt{a^2-\frac{1}{49}}\sqrt{b^2-\frac{1}{49}}
\]
Ako bismo $a+b+c$ prikazali kao $\frac{\sqrt{m}}{n}$ u maksimalno skraćenom obliku, koliko je $m+n$?
[/lang]
[lang=en]
After discussing some “chill” algebra problems, Ivica and Marica continue their conversation.
“I actually don’t like any algebra problem; all the other areas of mathematics are cool,” Marica proudly declared to Ivica. Upon hearing this, Ivica’s world began to fall apart, but he had a plan. He decided to give her five problems that are considered algebra, yet whose solutions are not necessarily algebraic, thereby showing her that algebra is the best field.
For the first problem, Ivica told Marica the following:
Let $a, b, c$ be \textbf{positive} real numbers satisfying the following equations:
\[
a^2=b^2+c^2-\frac{2}{25}+2\sqrt{b^2-\frac{1}{25}}\sqrt{c^2-\frac{1}{25}}
\]
\[
b^2=c^2+a^2-\frac{2}{36}+2\sqrt{a^2-\frac{1}{36}}\sqrt{c^2-\frac{1}{36}}
\]
\[
c^2=a^2+b^2-\frac{2}{49}+2\sqrt{a^2-\frac{1}{49}}\sqrt{b^2-\frac{1}{49}}
\]
If we express $a + b + c$ as $\frac{\sqrt{m}}{n}$ in lowest terms, what is the value of $m + n$?
[/lang]
 budu pozitivni realni brojevi za koje vrijedi sljedeće:
budu pozitivni realni brojevi za koje vrijedi sljedeće: 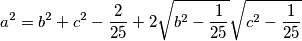
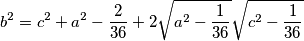
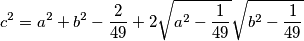 Ako bismo
Ako bismo 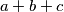 prikazali kao
prikazali kao 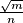 u maksimalno skraćenom obliku, koliko je
u maksimalno skraćenom obliku, koliko je  ?
?  be positive real numbers satisfying the following equations:
be positive real numbers satisfying the following equations: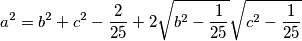
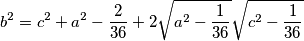
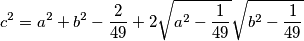
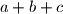 as
as 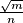 in lowest terms, what is the value of
in lowest terms, what is the value of 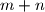 ?
? 