Vrijeme: 19:30
Fibonacci fun party #1
Društvo mladih matematičara došlo je na veliki i zabavni matematički party. Tamo je glavna atrakcija bio mađioničar Fibonacci. Srećom za naše matematičare (i na žalost svih ostalih prisutnih) Fibonacci nije izvlačio zečeve iz šešira, već matematičke zadatke. Tako je na početku zabave mađioničar Fibonacci za mlade matematičare izvukao jedan zadatak dobrodošlice.
Odredite najmanji prirodni broj  koji se ne može napisati kao zbroj Fibonaccijevih brojeva različitih indeksa, ukoliko je u prikazu zabranjena uporaba brojeva
koji se ne može napisati kao zbroj Fibonaccijevih brojeva različitih indeksa, ukoliko je u prikazu zabranjena uporaba brojeva 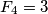 i
i 
Fibonaccijevi brojevi su brojevi koji zadovoljavaju rekurzivnu relaciju 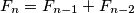 i za koje vrijedi
i za koje vrijedi 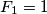
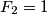 . Ovako će biti definirani i u ostatku zadataka ovog lanca
. Ovako će biti definirani i u ostatku zadataka ovog lanca
The society of young enthusiastic mathematicians gathered up for a big and super fun mathematical party. The main star of the show at the party was the mathemagician Fibonacci. Fibonacci's grand trcik was pulling out mathematical tasks for our math enthusiasts. So for a warmhearted welcome he pulled out the next task:
Find the smallest natural number which cannot be expressed as a sum of Fibonnaci number that all have a different index, if the expression mustn't contain the numbers
which cannot be expressed as a sum of Fibonnaci number that all have a different index, if the expression mustn't contain the numbers 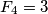 and
and 
Remark: Fibonacci numbers are numbers that satisfy the recursive relation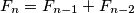 and for which
and for which 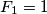
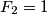 . This is also how the Fibonacci numbers will be defined in the rest of this chain.
. This is also how the Fibonacci numbers will be defined in the rest of this chain.
Find the smallest natural number
 which cannot be expressed as a sum of Fibonnaci number that all have a different index, if the expression mustn't contain the numbers
which cannot be expressed as a sum of Fibonnaci number that all have a different index, if the expression mustn't contain the numbers 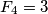 and
and 
Remark: Fibonacci numbers are numbers that satisfy the recursive relation
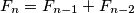 and for which
and for which 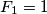
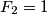 . This is also how the Fibonacci numbers will be defined in the rest of this chain.
. This is also how the Fibonacci numbers will be defined in the rest of this chain. 