Vrijeme: 19:29
Weirdgebra #5
Ivici je sada još ostao samo posljednji zadatak. Budući da do sada još nije postavio niti jedno pitanje o (nestandardnim) funkcijskim jednadžbama (a pred Maricom želi ispasti pametan), odlučio je da je upravo sada pravi trenutak za to. Kao svoj posljednji izazov Marici, Ivica govori:
Ako mi za funkciju 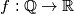 vrijedi
vrijedi 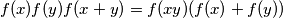 za sve
za sve 
Odredi zbroj svhim mogućih vrijednosti 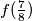 (zapiši rješenje u obliku maksimalno skraćenog razlomka
(zapiši rješenje u obliku maksimalno skraćenog razlomka 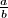 te kao odgovor na ovaj zadatak napiši vrijednost
te kao odgovor na ovaj zadatak napiši vrijednost  ).
).
Ivica now has only his final task left. Since he hasn't yet asked any question about (non‑standard) functional equations (and wants to appear clever in front of Marica), he decided that now is the perfect moment for it. As his last challenge to Marica, Ivica says:
If for a function 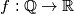 we have
we have 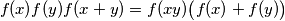 for all
for all 
Determine the sum of all possible values of 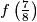 (write the solution in the form of a maximally reduced fraction
(write the solution in the form of a maximally reduced fraction 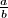 and, as the answer to this problem, give the value
and, as the answer to this problem, give the value  ).
).
