Marinada '25

[lang=hr] Na istom predavanju iz analize Ivica se skupio hrabrosti prići Marici. Budući da ih uopće nije bilo briga što se zapravo događa na predavanju, Ivica i Marica (na Ivicino oduševljenje) počeli su razgovarati o natjecateljskim zadatcima iz algebre. Budući da je Marica ispala tako chill, nije joj više htio podijeliti one stare \textit{lagane} zadatke, već nove \textit{chill} algebarske zadatke. 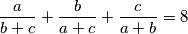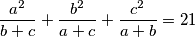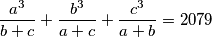Kao prvi \textit{chill} zadatak, zadao joj je sljedeće: Neka su $a,b,c$ kompleksni brojevi za koje vrijedi: \[ \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=8 \] \[ \frac{a^2}{b+c}+\frac{b^2}{a+c}+\frac{c^2}{a+b}=21 \] \[ \frac{a^3}{b+c}+\frac{b^3}{a+c}+\frac{c^3}{a+b}=2079 \] Odredi vrijednost izraza 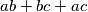$ab+bc+ac$ (rješenje zapiši kao potpuno skraćeni razlomak 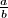$\frac{a}{b}$ te kao odgovor na ovo pitanje napiši vrijednost izraza $a+b$) [/lang] [lang=en] On the same lecture in analysis, Ivica gathered the courage to approach Marica. Since they didn’t care at all about what was actually happening in the lecture, Ivica and Marica (to Ivica’s delight) started talking about competition problems from algebra. Because Marica turned out to be so chill, he no longer wanted to give her the old easy problems, but rather new “chill” algebra problems. 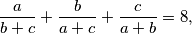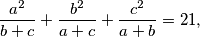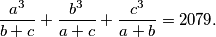As the first chill problem, he gave her the following: Let $a,b,c$ be complex numbers that satisfy $$\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=8,$$ $$\frac{a^{2}}{b+c}+\frac{b^{2}}{a+c}+\frac{c^{2}}{a+b}=21,$$ $$\frac{a^{3}}{b+c}+\frac{b^{3}}{a+c}+\frac{c^{3}}{a+b}=2079.$$ Determine the value of the expression 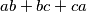$ab+bc+ca$. 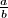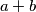Write the result as a completely reduced fraction $\frac{a}{b}$ and, as the answer to this question, give the value of the expression $a + b$. [/lang]