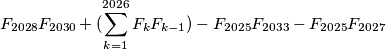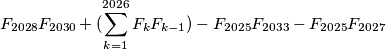I tako zabava ide dalje svojim tokom, a
Fibonacciju ne ponestaje zadataka iz šešira. Već je sad okupio veću publiku pa je vrijeme da iz šešira izvadi jedan možda malo teži zadatak kako bi impresionirao svoju publiku. Zadatak koji je izvadio glasi
Izračunaj izraz: 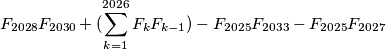
The party continues on and
Fibonacci is pulling the problems out of his hat like there is an infinite amount of them. He has now gathered quite a large audience so he thinks this is a right time to pull out a little bit more difficult task so he could impress his audience. And the task he pulled out iiiisss...:
Calculate the expression 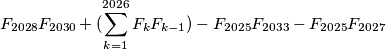
[lang=hr]
I tako zabava ide dalje svojim tokom, a \emph{Fibonacciju} ne ponestaje zadataka iz šešira. Već je sad okupio veću publiku pa je vrijeme da iz šešira izvadi jedan možda malo teži zadatak kako bi impresionirao svoju publiku. Zadatak koji je izvadio glasi
Izračunaj izraz:
$$F_{2028}F_{2030}+(\sum^{2026}_{k=1}F_kF_{k-1}) -F_{2025}F_{2033}-F_{2025}F_{2027}$$
[/lang]
[lang=en]
The party continues on and \emph{Fibonacci} is pulling the problems out of his hat like there is an infinite amount of them. He has now gathered quite a large audience so he thinks this is a right time to pull out a little bit more difficult task so he could impress his audience. And the task he pulled out iiiisss...:
Calculate the expression $$F_{2028}F_{2030}+(\sum^{2026}_{k=1}F_kF_{k-1}) -F_{2025}F_{2033}-F_{2025}F_{2027}$$
[/lang]