Vrijeme: 19:29
Chillgebra #3
Budući da je Marica s lakoćom riješila prošla dva chill zadatka, Ivica je odlučio Marici početi zadavati malo zahtjevnije zadatke, odnosno napete chill zadatke. Kao prvi takav zadatak, Ivica Marici postavlja:
Pronađi najveći nenegativni realni broj 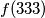 sa sljedećim svojstvom:
sa sljedećim svojstvom:
Kad god su 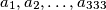 realni brojevi takvi da
realni brojevi takvi da 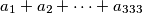 je cijeli broj, onda postoji neki
je cijeli broj, onda postoji neki  takav da
takav da
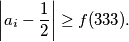
Zapiši 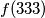 kao potpuno skraćeni razlomak
kao potpuno skraćeni razlomak 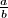 te kao odgovor na ovo pitanje zapiši vrijednost izraza
te kao odgovor na ovo pitanje zapiši vrijednost izraza 
Since Marica easily solved the previous two chill problems, Ivica decided to give her slightly harder tasks, i.e. tight‑chill problems. As the first such task Ivica asks Marica:
Find the greatest non‑negative real number 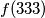 with the following property:
with the following property:
Whenever 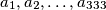 are real numbers whose sum
are real numbers whose sum 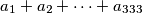 is an integer, there exists an index
is an integer, there exists an index  such that
such that

Write 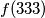 as a fully reduced fraction
as a fully reduced fraction 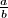 and answer the question with the value of the expression
and answer the question with the value of the expression  .
.
