Vrijeme: 19:30
Chillgebra #4
Budući da se je Marica jako namučila pokušavajući riješiti prošli napeti chill zadatak, odlučio joj je dati jedan poznatiji zadatak:
Pronađi najmanju konstantu 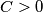 za koju vrijedi sljedeća tvrdnja:
za koju vrijedi sljedeća tvrdnja:
Između bilo kojih pet pozitivnih realnih brojeva 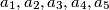 (ne nužno različitih), moguće je odabrati različite
(ne nužno različitih), moguće je odabrati različite 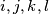 tako da vrijedi
tako da vrijedi
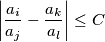
Rješenje za ovaj zadatak zapiši kao maksimalno skraćeni razlomak 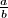 te kao rješenje na ovaj zadatak zapiši vrijednost
te kao rješenje na ovaj zadatak zapiši vrijednost 
Since Marica struggled a lot trying to solve the previous “tense‑chill” problem, she was given a better‑known one instead:
Find the smallest constant 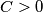 for which the following statement holds:
for which the following statement holds:
For any five positive real numbers 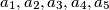 (not necessarily distinct), it is possible to choose four different indices
(not necessarily distinct), it is possible to choose four different indices 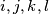 such that
such that
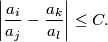
Write the solution for this problem as a fully reduced fraction 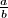 and, as the answer to the problem, give the value
and, as the answer to the problem, give the value  .
.
