Vrijeme: 19:27
Chillgebra #5
Nakon što je Marica automatski riješila prošli zadatak (nekoristeći internetske stranice), Ivica postavlja svoj posljednji zadatak. Prije govorenja tvrdnje, Ivica upozorava Maricu da je riječ o super napetom chill zadatku te da je u redu ako odustane. Međutim, Marica nije obeshrabrena te sluša Ivicinu postavku zadatka:
Neka 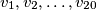 budu realni brojevi takvi da vrijedi
budu realni brojevi takvi da vrijedi

Pronađi sumu svih mogućih rješenja (uzimamo 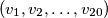 i
i 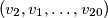 kao dva različita rješenja ako
kao dva različita rješenja ako 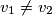 )
)
Rješenja zapiši kao razlomak 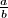 u potpuno skraćenom obliku te kao odgovor na ovo pitanje stavite
u potpuno skraćenom obliku te kao odgovor na ovo pitanje stavite  .
.
After Marica automatically solved the previous problem (without using any websites), Ivica presents her with his final challenge. Before stating the claim, Ivica warns Marica that this is a super tense chill problem and that it’s okay to give up. However, Marica is undeterred and listens to Ivica’s problem description:
Let 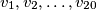 be real numbers satisfying
be real numbers satisfying
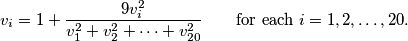
Find the sum of all possible solutions (treat 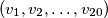 and
and 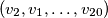 as two distinct solutions if
as two distinct solutions if 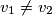 ).
).
Express solution as a reduced fraction 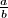 . As the answer to this question, submit the value
. As the answer to this question, submit the value  .
.
