Marinada '25

[lang=hr] Eeee ne mogu vjerovat! Znači ne volim tigonometriju, onak triggering mi je kad god čujem tu riječ. I onda danas dođe profa i zada nam za zadaću čak PETTT zadataka, i to ne samo iz trigonometrije, nego iz TRIGONOMETRIJSKIH NEJEDNAKOSTI!!! Like, ne znam hoću li preživjeti to, nemam energije za pet trig zadatakaaa! Ajde ovaj prvi se ne čini toliko strašan: Odredi najveću moguću vrijednost koju može poprimiti izraz 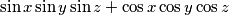$$\sin x \sin y \sin z + \cos x \cos y \cos z$$ za neke realne brojeve $x$, $y$ i $z$. Ako je odgovor u obliku razlomka, skrati ga i napiši mu zbroj brojnika i nazivnika [/lang] [lang=en] I can’t believe it! So I don’t like “tigonometry”; it just triggers me whenever I hear that word. And then today the professor gave us five homework problems, not only from trigonometry but also from trigonometric inequalities!!! I don’t know if I’ll survive this; I have no energy for five trig problems! 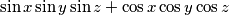Let’s start with the first one—it doesn’t seem that terrifying: Determine the greatest possible value that the expression $$ \sin x \sin y \sin z + \cos x \cos y \cos z $$ can take for some real numbers $x$, $y$ and $z$. If the answer is a fraction, reduce it and write the sum of its numerator and denominator. [/lang]