Vrijeme: 19:27
TRIGgggering nejednakosti | TRIGgggering inequalities #3
Ajme što je bio ovaj prijašnji zadatak??. Ajde još nisam pao u nesvijest, idemo vidjeti može li me sljedeći zadatak nokautirati. Možda i može...
Neka su 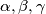 kutovi netupokutnog trokuta, a
kutovi netupokutnog trokuta, a  i
i  polumjeri njemu opisane i upisane kružnice. Nađi najveći
polumjeri njemu opisane i upisane kružnice. Nađi najveći  tako da uvijek vrijedi nejednakost
tako da uvijek vrijedi nejednakost 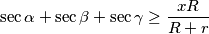 . U polje za odgovore upiši
. U polje za odgovore upiši  . Ako je
. Ako je  razlomak zapiši ga u skraćenom obliku
razlomak zapiši ga u skraćenom obliku 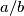 te u polje upiši umnožak
te u polje upiši umnožak  . Ako je rezultat koji bi upisao u polje jako velik izračunaj njegov ostatak pri dijeljenju s
. Ako je rezultat koji bi upisao u polje jako velik izračunaj njegov ostatak pri dijeljenju s 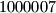 .
.
What was that previous problem? Come on, I haven’t fainted yet; let’s see if the next problem can knock me out. Maybe it can…
Let 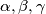 be the angles of an acute‑angled triangle, and let
be the angles of an acute‑angled triangle, and let  and
and  be the radii of its circumcircle and incircle, respectively. Find the largest constant
be the radii of its circumcircle and incircle, respectively. Find the largest constant  such that the inequality
such that the inequality
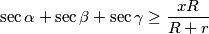
holds for every acute‑angled triangle.
Enter 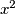 in the answer box. If
in the answer box. If 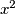 is a fraction, write it in lowest terms as
is a fraction, write it in lowest terms as 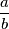 and then enter the product
and then enter the product  in the answer box. If the resulting number is very large, compute its remainder modulo
in the answer box. If the resulting number is very large, compute its remainder modulo 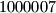 .
.
