Nedaaa mi se više!! Kolikooo još imam???. geeez još dva zadatka. Ajde jedan brzinski cofffffe break pa ću nastavit
..................................................................................................................................................................................
Ok idemoo daljeee! Ili možda bolje ne...
Odredite maksimum funkcije 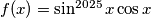
Za odgovor na ovaj zadatak za taj  za koji se postiže maksimalna vrijednost izračunajte
za koji se postiže maksimalna vrijednost izračunajte 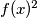 . Koji god broj dobijete pretvorite ga u potpuno skraćeni oblik razlomka
. Koji god broj dobijete pretvorite ga u potpuno skraćeni oblik razlomka 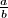 .(znači ako je cijeli broj,
.(znači ako je cijeli broj, 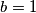 , a
, a  je jednak tom cijelom broju)
je jednak tom cijelom broju)
Izračunajte  . Ako je broj jako velik zapišite njegov ostatak pri dijeljenju s
. Ako je broj jako velik zapišite njegov ostatak pri dijeljenju s 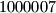 .
.
[lang=hr]
Nedaaa mi se više!! Kolikooo još imam???. geeez još dva zadatka. Ajde jedan brzinski cofffffe break pa ću nastavit
..................................................................................................................................................................................
Ok idemoo daljeee! Ili možda bolje ne...
Odredite maksimum funkcije $f(x)=\sin^{2025}x\cos x$
Za odgovor na ovaj zadatak za taj $x$ za koji se postiže maksimalna vrijednost izračunajte $f(x)^2$. Koji god broj dobijete pretvorite ga u potpuno skraćeni oblik razlomka $\frac{a}{b}$.(znači ako je cijeli broj, $b=1$, a $a$ je jednak tom cijelom broju)
Izračunajte $a+b$. Ako je broj jako velik zapišite njegov ostatak pri dijeljenju s $1000007$.
[/lang]
[lang=en]
I don’t feel like doing anything anymore!! How many more do I have??? Geez, two more problems. Let’s take a quick coffee break and then I’ll continue.
..............................................................................................................................................................................
Okay, I’m moving on! Or maybe it’s better not to…
Determine the maximum of the function
$f(x)=\sin^{2025}x\cos x $
For the value of $x$ at which the maximum is attained, compute $f(x)^2$. Write whatever number you obtain as a fully reduced fraction $\dfrac{a}{b}$ (so if it is an integer, set $b=1$ and $a$ equals that integer).
Calculate $a + b$. If the number is very large, give its remainder upon division by $1000007$.
[/lang]
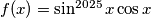
 za koji se postiže maksimalna vrijednost izračunajte
za koji se postiže maksimalna vrijednost izračunajte 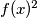 . Koji god broj dobijete pretvorite ga u potpuno skraćeni oblik razlomka
. Koji god broj dobijete pretvorite ga u potpuno skraćeni oblik razlomka 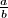 .(znači ako je cijeli broj,
.(znači ako je cijeli broj, 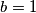 , a
, a  je jednak tom cijelom broju)
je jednak tom cijelom broju) . Ako je broj jako velik zapišite njegov ostatak pri dijeljenju s
. Ako je broj jako velik zapišite njegov ostatak pri dijeljenju s 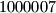 .
. 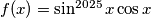
 at which the maximum is attained, compute
at which the maximum is attained, compute 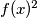 . Write whatever number you obtain as a fully reduced fraction
. Write whatever number you obtain as a fully reduced fraction 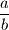 (so if it is an integer, set
(so if it is an integer, set 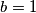 and
and  equals that integer).
equals that integer).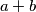 . If the number is very large, give its remainder upon division by
. If the number is very large, give its remainder upon division by 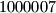 .
.