I tako, kako je Karlo razmišljao o dubokoumnim temama, počeo je razmišljati o četverodimenzionalnom prostoru i kakav bi to bio život u 4D.
Za početak si je vizualizirao 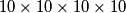 hiperkocku i rekao ovako: "Neka jedna hiperkockica dimenzija
hiperkocku i rekao ovako: "Neka jedna hiperkockica dimenzija 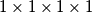 koja je u kutu originalne hiperkocke bude upaljena. Nakon jedne minute se ta hiperkockica gasi i pale se njoj susjedne hiperkockice. Ovaj proces paljenja susjednih hiperkockica i gašenje upaljenih hiperkockica se nastavlja. Kada će se po prvi puta dogoditi da se ponovi ista konstrukcija? (dvije hiperkocke imaju istu konstrukciju ako je svaka hiperkockica koja je upaljena u prvoj hiperkocki ujedno upaljena i u drugoj hiperkocki, isto vrijedi i za ugašene hiperkockice)"
koja je u kutu originalne hiperkocke bude upaljena. Nakon jedne minute se ta hiperkockica gasi i pale se njoj susjedne hiperkockice. Ovaj proces paljenja susjednih hiperkockica i gašenje upaljenih hiperkockica se nastavlja. Kada će se po prvi puta dogoditi da se ponovi ista konstrukcija? (dvije hiperkocke imaju istu konstrukciju ako je svaka hiperkockica koja je upaljena u prvoj hiperkocki ujedno upaljena i u drugoj hiperkocki, isto vrijedi i za ugašene hiperkockice)"
Note: Hiperkockica u kutu ima četiri susjedne hiperkockice, a hiperkockica u srednjem dijelu hiperkocke ima 8 susjednih hiperkockica.
As Karlo pondered deep and profound questions, he began to think about four-dimensional space and what life might be like in
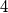
D.
To begin, he visualized a 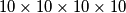 hypercube and said:
hypercube and said:
"Let one unit hypercube of size 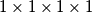 , located at a corner of the original hypercube, be activated. After one minute, that hypercube turns off and all of its neighboring hypercubes get activated. This process of activating neighbours and deactivating active unit hypercubes continues. When will it happen, for the first time, that the configuration repeats itself? (Two hypercubes are considered to have the same configuration if every hypercube that is active in the first configuration is also active in the second, and vice versa.)"
, located at a corner of the original hypercube, be activated. After one minute, that hypercube turns off and all of its neighboring hypercubes get activated. This process of activating neighbours and deactivating active unit hypercubes continues. When will it happen, for the first time, that the configuration repeats itself? (Two hypercubes are considered to have the same configuration if every hypercube that is active in the first configuration is also active in the second, and vice versa.)"
Note. A unit hypercube located in a corner has 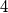 neighboring hypercubes, while a unit hypercube in the interior of the hypercube has
neighboring hypercubes, while a unit hypercube in the interior of the hypercube has 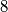 neighboring hypercubes.
neighboring hypercubes.
[lang=hr]
I tako, kako je Karlo razmišljao o dubokoumnim temama, počeo je razmišljati o četverodimenzionalnom prostoru i kakav bi to bio život u 4D.
Za početak si je vizualizirao $10 \times 10 \times 10 \times 10$ hiperkocku i rekao ovako: "Neka jedna hiperkockica dimenzija $1\times 1\times 1 \times 1$ koja je u kutu originalne hiperkocke bude upaljena. Nakon jedne minute se ta hiperkockica gasi i pale se njoj susjedne hiperkockice. Ovaj proces paljenja susjednih hiperkockica i gašenje upaljenih hiperkockica se nastavlja. Kada će se po prvi puta dogoditi da se ponovi ista konstrukcija? (dvije hiperkocke imaju istu konstrukciju ako je svaka hiperkockica koja je upaljena u prvoj hiperkocki ujedno upaljena i u drugoj hiperkocki, isto vrijedi i za ugašene hiperkockice)"
Note: Hiperkockica u kutu ima četiri susjedne hiperkockice, a hiperkockica u srednjem dijelu hiperkocke ima 8 susjednih hiperkockica.
[/lang]
[lang=en]
As Karlo pondered deep and profound questions, he began to think about four-dimensional space and what life might be like in \(4\)D.
To begin, he visualized a \(10 \times 10 \times 10 \times 10\) hypercube and said:
\emph{"Let one unit hypercube of size \(1 \times 1 \times 1 \times 1\), located at a corner of the original hypercube, be activated. After one minute, that hypercube turns off and all of its neighboring hypercubes get activated. This process of activating neighbours and deactivating active unit hypercubes continues. When will it happen, for the first time, that the configuration repeats itself? (Two hypercubes are considered to have the same configuration if every hypercube that is active in the first configuration is also active in the second, and vice versa.)"}
\textbf{Note.} A unit hypercube located in a corner has \(4\) neighboring hypercubes, while a unit hypercube in the interior of the hypercube has \(8\) neighboring hypercubes.
[/lang]
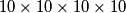 hiperkocku i rekao ovako: "Neka jedna hiperkockica dimenzija
hiperkocku i rekao ovako: "Neka jedna hiperkockica dimenzija 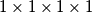 koja je u kutu originalne hiperkocke bude upaljena. Nakon jedne minute se ta hiperkockica gasi i pale se njoj susjedne hiperkockice. Ovaj proces paljenja susjednih hiperkockica i gašenje upaljenih hiperkockica se nastavlja. Kada će se po prvi puta dogoditi da se ponovi ista konstrukcija? (dvije hiperkocke imaju istu konstrukciju ako je svaka hiperkockica koja je upaljena u prvoj hiperkocki ujedno upaljena i u drugoj hiperkocki, isto vrijedi i za ugašene hiperkockice)"
koja je u kutu originalne hiperkocke bude upaljena. Nakon jedne minute se ta hiperkockica gasi i pale se njoj susjedne hiperkockice. Ovaj proces paljenja susjednih hiperkockica i gašenje upaljenih hiperkockica se nastavlja. Kada će se po prvi puta dogoditi da se ponovi ista konstrukcija? (dvije hiperkocke imaju istu konstrukciju ako je svaka hiperkockica koja je upaljena u prvoj hiperkocki ujedno upaljena i u drugoj hiperkocki, isto vrijedi i za ugašene hiperkockice)"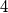 D.
D.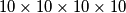 hypercube and said:
hypercube and said: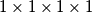 , located at a corner of the original hypercube, be activated. After one minute, that hypercube turns off and all of its neighboring hypercubes get activated. This process of activating neighbours and deactivating active unit hypercubes continues. When will it happen, for the first time, that the configuration repeats itself? (Two hypercubes are considered to have the same configuration if every hypercube that is active in the first configuration is also active in the second, and vice versa.)"
, located at a corner of the original hypercube, be activated. After one minute, that hypercube turns off and all of its neighboring hypercubes get activated. This process of activating neighbours and deactivating active unit hypercubes continues. When will it happen, for the first time, that the configuration repeats itself? (Two hypercubes are considered to have the same configuration if every hypercube that is active in the first configuration is also active in the second, and vice versa.)"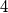 neighboring hypercubes, while a unit hypercube in the interior of the hypercube has
neighboring hypercubes, while a unit hypercube in the interior of the hypercube has 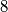 neighboring hypercubes.
neighboring hypercubes. 