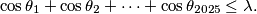Yes yes yes yessssss!!!!! Riješio sam skoro sve zadatkeeee!!
Samo još jedan, samo još jedan mali zadatčićć.
WAITTTT!?!?, jeli profa luda, kako da itko ovo riješi??????
Odredi najmanji realni broj 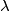 tako da za bilo koji
tako da za bilo koji 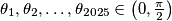 , ako
, ako 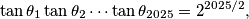 onda
onda 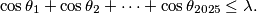
Yes yes yes yessssss!!!!! I’ve solved almost all the problems!!!
Just one more, just one tiny little problem.
WAIT!!! Is the professor crazy, how could anyone solve this???
Determine the smallest positive real number 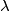 such that for any
such that for any 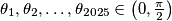 , if
, if 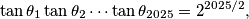 then
then 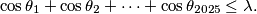
[lang=hr]
Yes yes yes yessssss!!!!! Riješio sam skoro sve zadatkeeee!!
Samo još jedan, samo još jedan mali zadatčićć.
WAITTTT!?!?, jeli profa luda, kako da itko ovo riješi??????
Odredi najmanji realni broj $\lambda$ tako da za bilo koji $\theta_1, \theta_2, \ldots, \theta_{2025} \in \left(0, \frac{\pi}{2}\right)$, ako
\[
\tan \theta_1 \tan \theta_2 \cdots \tan \theta_{2025} = 2^{2025/2},
\]
onda
\[
\cos \theta_1 + \cos \theta_2 + \cdots + \cos \theta_{2025} \le \lambda.
\]
[/lang]
[lang=en]
Yes yes yes yessssss!!!!! I’ve solved almost all the problems!!!
Just one more, just one tiny little problem.
WAIT!!! Is the professor crazy, how could anyone solve this???
Determine the smallest positive real number $\lambda$ such that for any $\theta_1, \theta_2, \ldots, \theta_{2025} \in \left(0, \frac{\pi}{2}\right)$, if
\[
\tan \theta_1 \tan \theta_2 \cdots \tan \theta_{2025} = 2^{2025/2},
\]
then
\[
\cos \theta_1 + \cos \theta_2 + \cdots + \cos \theta_{2025}\le \lambda.
\]
[/lang]
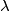 tako da za bilo koji
tako da za bilo koji 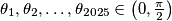 , ako
, ako 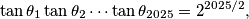 onda
onda 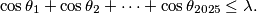
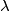 such that for any
such that for any 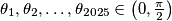 , if
, if 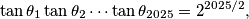 then
then