Vrijeme: 19:27
Četverodimenzionalna komba | 4D Combinatorics #2
Ova 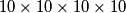 hiperkocka je previše za razmišljat. Zbog toga, Karlo je počeo razmatrati nešto manju hiperkocku koja ima dimenzije
hiperkocka je previše za razmišljat. Zbog toga, Karlo je počeo razmatrati nešto manju hiperkocku koja ima dimenzije 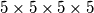 . Za ovu hiperkocku Karla zanima sljedeće:
. Za ovu hiperkocku Karla zanima sljedeće:
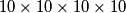 hiperkocka je previše za razmišljat. Zbog toga, Karlo je počeo razmatrati nešto manju hiperkocku koja ima dimenzije
hiperkocka je previše za razmišljat. Zbog toga, Karlo je počeo razmatrati nešto manju hiperkocku koja ima dimenzije 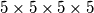 . Za ovu hiperkocku Karla zanima sljedeće:
. Za ovu hiperkocku Karla zanima sljedeće:Ako bi krenio iz kutne hiperkockice, na koliko načina može doći do dijagonalno nasuprotne hiperkockice ako se vrijednosti svih četiriju koordinata smiju samo povećavati? (pretpostavljamo da putanja kreće u 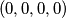 i da se hiperkocka širi u pozitivnome smjeru svih koordinatnih osi).
i da se hiperkocka širi u pozitivnome smjeru svih koordinatnih osi).
This 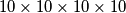 hypercube is too large to think about. Therefore Karlo began considering a smaller hypercube of dimensions
hypercube is too large to think about. Therefore Karlo began considering a smaller hypercube of dimensions 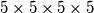 . For this hypercube Karlo wonders the following:
. For this hypercube Karlo wonders the following:
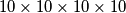 hypercube is too large to think about. Therefore Karlo began considering a smaller hypercube of dimensions
hypercube is too large to think about. Therefore Karlo began considering a smaller hypercube of dimensions 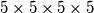 . For this hypercube Karlo wonders the following:
. For this hypercube Karlo wonders the following:If he starts from a corner unit hypercube, in how many ways can he reach the diagonally opposite unit hypercube if the values of all four coordinates are only allowed to increase? (We assume the path starts at 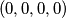 and that the hypercube extends in the positive direction along each coordinate axis.)
and that the hypercube extends in the positive direction along each coordinate axis.)
