Okej, Karlo je sad počeo shvačati kako je ta četverodimenzionalna hiper kocka prožeta i povezana. Sada Karlo odlučuje promatrati
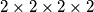
hiperkocku te si postavlja pitanje:
Ako svakoj hiperkockici dodam strijelicu koja pokazuje na neku susjednu hiperkockicu, na koliko načina mogu pridodati strijelice svim hiperkockicama tako da svaka hiperkockica ima neku susjednu hiperkockicu koja pokazuje na nju.
Note: dva postavljanja strijelica u hiperkocki se uzimaju kao različita čak ako se međusobno mogu dobiti rotacijom ili simetrijom.
Karlo is now beginning to understand how interconnected and linked this four-dimensional hypercube is. He now decides to consider a

hypercube and asks himself the following question:
If we add an arrow to each unit hypercube pointing to one of its neighboring unit hypercubes, in how many ways can we assign arrows to all unit hypercubes such that every unit hypercube has at least one neighboring unit hypercube pointing to it?
Note. Two arrow assignments in the hypercube are considered different even if they can be obtained from one another by rotation or reflection (symmetry).
[lang=hr]
Okej, Karlo je sad počeo shvačati kako je ta četverodimenzionalna hiper kocka prožeta i povezana. Sada Karlo odlučuje promatrati $2 \times 2 \times 2 \times 2$ hiperkocku te si postavlja pitanje:
Ako svakoj hiperkockici dodam strijelicu koja pokazuje na neku susjednu hiperkockicu, na koliko načina mogu pridodati strijelice svim hiperkockicama tako da svaka hiperkockica ima neku susjednu hiperkockicu koja pokazuje na nju.
Note: dva postavljanja strijelica u hiperkocki se uzimaju kao različita čak ako se međusobno mogu dobiti rotacijom ili simetrijom.
[/lang]
[lang=en]
Karlo is now beginning to understand how interconnected and linked this four-dimensional hypercube is. He now decides to consider a \(2\times 2\times 2\times 2\) hypercube and asks himself the following question:
If we add an arrow to each unit hypercube pointing to one of its neighboring unit hypercubes, in how many ways can we assign arrows to all unit hypercubes such that every unit hypercube has at least one neighboring unit hypercube pointing to it?
\textbf{Note.} Two arrow assignments in the hypercube are considered different even if they can be obtained from one another by rotation or reflection (symmetry).
[/lang]
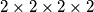 hiperkocku te si postavlja pitanje:
hiperkocku te si postavlja pitanje: hypercube and asks himself the following question:
hypercube and asks himself the following question: