Vrijeme: 19:27
Četverodimenzionalna komba | 4D Combinatorics #5
Karlo je zatim počeo razmišljati kako bi cijelom ovom dubokoumnom lancu htio dati poučan završetak i podučiti čitatelja kako rješavati olimpijske zadatke koristeći 4D prostor. Puno stvari u životu može biti simulirano u 4D (n-D) prostoru. Naprimjer, četveroznamenkasti pin može biti prikazan kao 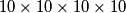 hiperkocka (uzevši u obzir da uubacujemo znamenke od
hiperkocka (uzevši u obzir da uubacujemo znamenke od  do
do  ). Naravno, kompleksni kombinatorni zadatci se uglavnom olakšaju kad se vizualiziraju (misli IMO 2024 P3). Jedan problem koji showcasea ovu ideju (i u duhu je ovog lanca) je sljedeći:
). Naravno, kompleksni kombinatorni zadatci se uglavnom olakšaju kad se vizualiziraju (misli IMO 2024 P3). Jedan problem koji showcasea ovu ideju (i u duhu je ovog lanca) je sljedeći:
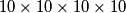 hiperkocka (uzevši u obzir da uubacujemo znamenke od
hiperkocka (uzevši u obzir da uubacujemo znamenke od  do
do  ). Naravno, kompleksni kombinatorni zadatci se uglavnom olakšaju kad se vizualiziraju (misli IMO 2024 P3). Jedan problem koji showcasea ovu ideju (i u duhu je ovog lanca) je sljedeći:
). Naravno, kompleksni kombinatorni zadatci se uglavnom olakšaju kad se vizualiziraju (misli IMO 2024 P3). Jedan problem koji showcasea ovu ideju (i u duhu je ovog lanca) je sljedeći:Uzmimo sve djeljitelje nekog  i poredajmo ih u niz tako da vrijedi da je barem jedan od
i poredajmo ih u niz tako da vrijedi da je barem jedan od 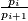 ili
ili 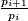 prost broj. Dokaži da je za bilo koji
prost broj. Dokaži da je za bilo koji  moguće tako poredati djelitelje (naprimjer, niz
moguće tako poredati djelitelje (naprimjer, niz 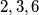 ne radi, ali
ne radi, ali 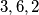 ) radi.
) radi.
Kad si dokazao ovo (a stvarno je cool dokaz ako koristiš n dimenzija), kao odgovor na ovo pitanje napiši "ok".
Karlo then began thinking about how he could give a meaningful conclusion to this deep chain of thoughts and teach the reader how to solve olympiad-style problems using 4D space. Many things in life can be simulated in 4D (or n-dimensional) space. For example, a four-digit PIN can be represented as a 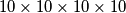 hypercube (taking into account that we insert digits from 0 to 9). Naturally, complex combinatorial problems are often easier to tackle when visualized (think IMO 2024 P3).
hypercube (taking into account that we insert digits from 0 to 9). Naturally, complex combinatorial problems are often easier to tackle when visualized (think IMO 2024 P3).
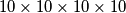 hypercube (taking into account that we insert digits from 0 to 9). Naturally, complex combinatorial problems are often easier to tackle when visualized (think IMO 2024 P3).
hypercube (taking into account that we insert digits from 0 to 9). Naturally, complex combinatorial problems are often easier to tackle when visualized (think IMO 2024 P3).One problem that showcases this idea (and is in the spirit of this chain) is the following:
Consider all the divisors of a positive integer 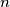 , and arrange them in a sequence such that for each consecutive pair
, and arrange them in a sequence such that for each consecutive pair 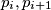 , at least one of the ratios
, at least one of the ratios 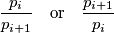 is a prime number. Prove that it is always possible to arrange the divisors of any
is a prime number. Prove that it is always possible to arrange the divisors of any 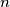 in such a sequence.
in such a sequence.
Example. The sequence 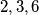 does not work, but
does not work, but 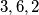 does.
does.
As the answer to this question, input "ok".
