Vrijeme: 19:29
Ploče! | Boards! #1
Želimo postaviti  polukraljica na šahovsku ploču dimenzija
polukraljica na šahovsku ploču dimenzija 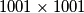 ; one mogu napadati vodoravno, okomito ili po dijagonali prema dolje-desno/gore-lijevo (tj. u šest smjerova), a napadaju i polje na kojem se nalaze. Odredite najmanji
; one mogu napadati vodoravno, okomito ili po dijagonali prema dolje-desno/gore-lijevo (tj. u šest smjerova), a napadaju i polje na kojem se nalaze. Odredite najmanji  takav da postoji raspored u kojem je svako polje na ploči napadnuto barem jednom polukraljicom.
takav da postoji raspored u kojem je svako polje na ploči napadnuto barem jednom polukraljicom.
 polukraljica na šahovsku ploču dimenzija
polukraljica na šahovsku ploču dimenzija 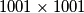 ; one mogu napadati vodoravno, okomito ili po dijagonali prema dolje-desno/gore-lijevo (tj. u šest smjerova), a napadaju i polje na kojem se nalaze. Odredite najmanji
; one mogu napadati vodoravno, okomito ili po dijagonali prema dolje-desno/gore-lijevo (tj. u šest smjerova), a napadaju i polje na kojem se nalaze. Odredite najmanji  takav da postoji raspored u kojem je svako polje na ploči napadnuto barem jednom polukraljicom.
takav da postoji raspored u kojem je svako polje na ploči napadnuto barem jednom polukraljicom. We want to place  semi-queens on a
semi-queens on a 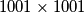 chessboard. A semi-queen can attack horizontally, vertically, and along the downward-right / upward-left diagonals (i.e., in six directions), and it also attacks the square it occupies. Determine the minimum
chessboard. A semi-queen can attack horizontally, vertically, and along the downward-right / upward-left diagonals (i.e., in six directions), and it also attacks the square it occupies. Determine the minimum  such that there exists an arrangement in which every square on the board is attacked by at least one semi-queen.
such that there exists an arrangement in which every square on the board is attacked by at least one semi-queen.
 semi-queens on a
semi-queens on a 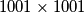 chessboard. A semi-queen can attack horizontally, vertically, and along the downward-right / upward-left diagonals (i.e., in six directions), and it also attacks the square it occupies. Determine the minimum
chessboard. A semi-queen can attack horizontally, vertically, and along the downward-right / upward-left diagonals (i.e., in six directions), and it also attacks the square it occupies. Determine the minimum  such that there exists an arrangement in which every square on the board is attacked by at least one semi-queen.
such that there exists an arrangement in which every square on the board is attacked by at least one semi-queen. 