Vrijeme: 19:30
Ploče! | Boards! #2
Nad svakom stranicom jednakostraničnog trokuta konstruiramo pravce paralelne stranici trokuta tako da visinu pripadane stranice dijeli na 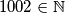 jednakih dijelova (skica za slučaj u kojem visinu pripadane stranice dijelimo na
jednakih dijelova (skica za slučaj u kojem visinu pripadane stranice dijelimo na  jednaka dijela nalazi se ispod). Na vrhove novonastalih manjih jednakostraničnih trokuta postavljaju se kraljice. Kraljica napada sve točke na čijim je pravcima (skica ispod, kraljica je Q). Koliko najviše kraljica, da se međusobno ne napadaju, možemo postaviti na danu ploču?
jednaka dijela nalazi se ispod). Na vrhove novonastalih manjih jednakostraničnih trokuta postavljaju se kraljice. Kraljica napada sve točke na čijim je pravcima (skica ispod, kraljica je Q). Koliko najviše kraljica, da se međusobno ne napadaju, možemo postaviti na danu ploču?
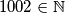 jednakih dijelova (skica za slučaj u kojem visinu pripadane stranice dijelimo na
jednakih dijelova (skica za slučaj u kojem visinu pripadane stranice dijelimo na  jednaka dijela nalazi se ispod). Na vrhove novonastalih manjih jednakostraničnih trokuta postavljaju se kraljice. Kraljica napada sve točke na čijim je pravcima (skica ispod, kraljica je Q). Koliko najviše kraljica, da se međusobno ne napadaju, možemo postaviti na danu ploču?
jednaka dijela nalazi se ispod). Na vrhove novonastalih manjih jednakostraničnih trokuta postavljaju se kraljice. Kraljica napada sve točke na čijim je pravcima (skica ispod, kraljica je Q). Koliko najviše kraljica, da se međusobno ne napadaju, možemo postaviti na danu ploču?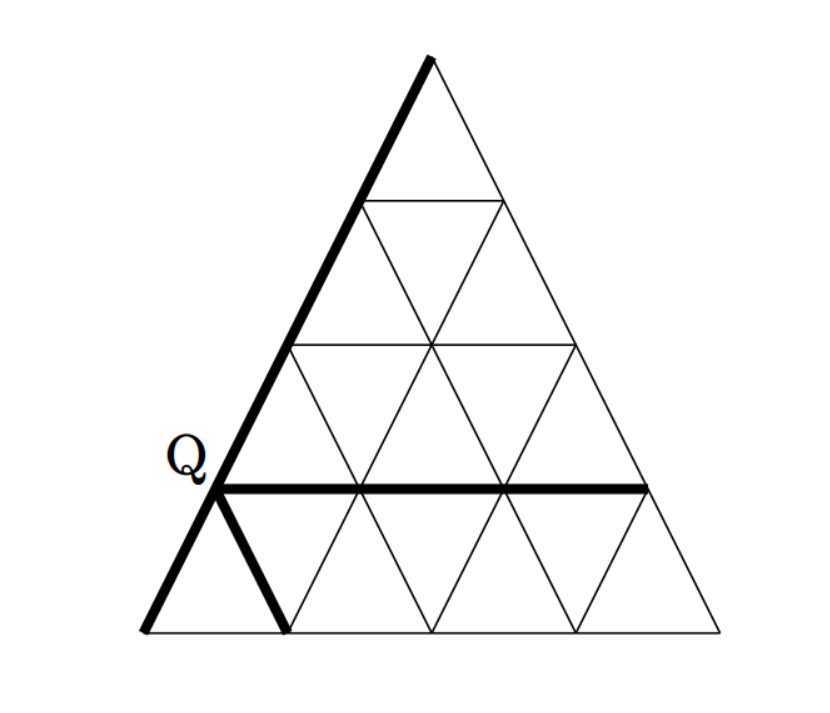
Above each side of an equilateral triangle, construct lines parallel to that side so that the altitude corresponding to that side is divided into 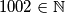 equal parts. (A sketch for the case where the altitude is divided into
equal parts. (A sketch for the case where the altitude is divided into 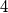 equal parts is shown below.)
equal parts is shown below.)
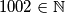 equal parts. (A sketch for the case where the altitude is divided into
equal parts. (A sketch for the case where the altitude is divided into 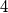 equal parts is shown below.)
equal parts is shown below.)Place queens at the vertices of the resulting smaller equilateral triangles. A queen attacks all points along the lines passing through it (see the sketch below, where the queen is marked 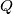 ).
).
What is the maximum number of queens that can be placed on the board so that no two attack each other?

