Vrijeme: 19:27
Ploče! | Boards! #3
Neka je  jednakostraničan trokut. Iz vrha
jednakostraničan trokut. Iz vrha  povlačimo pravac usmjeren prema unutarnjem dijelu trokuta tako da pravac dosegne suprotnu stranicu trokuta (
povlačimo pravac usmjeren prema unutarnjem dijelu trokuta tako da pravac dosegne suprotnu stranicu trokuta ( ). Kada pravac dođe do suprotne strane, ono se odbija prema pravilu refleksije. Nakon
). Kada pravac dođe do suprotne strane, ono se odbija prema pravilu refleksije. Nakon  sudara sa stranicama trokuta, pravac se vraća u
sudara sa stranicama trokuta, pravac se vraća u  bez da je ikada došao u vrhove
bez da je ikada došao u vrhove  i
i  . Odredi zbroj svih mogućić vrijednosti od
. Odredi zbroj svih mogućić vrijednosti od  koji su
koji su 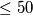 .
.
 jednakostraničan trokut. Iz vrha
jednakostraničan trokut. Iz vrha  povlačimo pravac usmjeren prema unutarnjem dijelu trokuta tako da pravac dosegne suprotnu stranicu trokuta (
povlačimo pravac usmjeren prema unutarnjem dijelu trokuta tako da pravac dosegne suprotnu stranicu trokuta ( ). Kada pravac dođe do suprotne strane, ono se odbija prema pravilu refleksije. Nakon
). Kada pravac dođe do suprotne strane, ono se odbija prema pravilu refleksije. Nakon  sudara sa stranicama trokuta, pravac se vraća u
sudara sa stranicama trokuta, pravac se vraća u  bez da je ikada došao u vrhove
bez da je ikada došao u vrhove  i
i  . Odredi zbroj svih mogućić vrijednosti od
. Odredi zbroj svih mogućić vrijednosti od  koji su
koji su 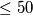 .
. Let 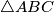 be an equilateral triangle. From vertex
be an equilateral triangle. From vertex 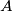 , we draw a line directed towards the interior of the triangle so that it reaches the opposite side
, we draw a line directed towards the interior of the triangle so that it reaches the opposite side 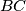 . When the line hits a side, it reflects according to the law of reflection. After
. When the line hits a side, it reflects according to the law of reflection. After 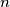 collisions with the sides of the triangle, the line returns to
collisions with the sides of the triangle, the line returns to 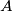 without ever hitting vertices
without ever hitting vertices 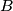 or
or 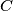 . Determine the sum of all possible values of
. Determine the sum of all possible values of 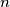 that are
that are 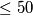 .
.
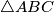 be an equilateral triangle. From vertex
be an equilateral triangle. From vertex 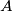 , we draw a line directed towards the interior of the triangle so that it reaches the opposite side
, we draw a line directed towards the interior of the triangle so that it reaches the opposite side 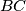 . When the line hits a side, it reflects according to the law of reflection. After
. When the line hits a side, it reflects according to the law of reflection. After 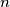 collisions with the sides of the triangle, the line returns to
collisions with the sides of the triangle, the line returns to 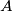 without ever hitting vertices
without ever hitting vertices 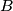 or
or 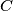 . Determine the sum of all possible values of
. Determine the sum of all possible values of 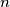 that are
that are 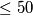 .
. 