Vrijeme: 19:30
Ploče! | Boards! #4
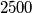 šahovskih kraljeva moraju biti postavljeni na
šahovskih kraljeva moraju biti postavljeni na 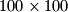 šahovsku ploču tako da vrijede sljedeći uvjeti:
šahovsku ploču tako da vrijede sljedeći uvjeti:  Pronađi broj načina na koji možemo postaviti kraljeve. (dva postavljanja kraljeva se uzimaju kao različita ako se međusobno mogu dobiti rotacijom ili simetrijom).
Pronađi broj načina na koji možemo postaviti kraljeve. (dva postavljanja kraljeva se uzimaju kao različita ako se međusobno mogu dobiti rotacijom ili simetrijom). Place 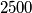 chess kings on a
chess kings on a 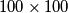 chessboard satisfying the following conditions:
chessboard satisfying the following conditions: 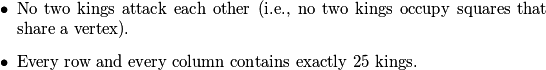 Find the number of ways to place the kings. (Two placements are considered different if they cannot be obtained from one another by rotation or reflection.)
Find the number of ways to place the kings. (Two placements are considered different if they cannot be obtained from one another by rotation or reflection.)
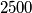 chess kings on a
chess kings on a 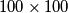 chessboard satisfying the following conditions:
chessboard satisfying the following conditions: 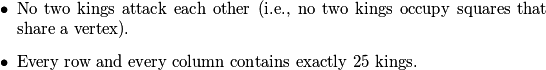 Find the number of ways to place the kings. (Two placements are considered different if they cannot be obtained from one another by rotation or reflection.)
Find the number of ways to place the kings. (Two placements are considered different if they cannot be obtained from one another by rotation or reflection.) 