Pri dijeljenju polinoma

s polinomom
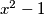
dobiva se ostatak. Nađi vrijednost varijable

za koju je numerička vrijednost tog ostatka jednaka

.
When dividing the polynomial

by the polynomial
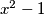
there is a remainder. Find the value of the variable

for which the numerical value of that remainder is

[lang=hr]
Pri dijeljenju polinoma
\[
x^3 + x^5 + x^7 + x^9 + x^{11} + x^{2017} + x^{2018}
\]
s polinomom \(x^2 - 1\) dobiva se ostatak.
Nađi vrijednost varijable \(x\) za koju je numerička vrijednost tog ostatka jednaka \(1111\).
[/lang]
[lang=en]
When dividing the polynomial $x^3+x^5+x^7+x^9+x^{11}+x^{2017}+x^{2018}$ by the polynomial $x^2-1$ there is a remainder. Find the value of the variable $x$ for which the numerical value of that remainder is $1111$
[/lang]