Ako
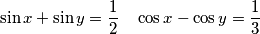
Koliko je
?
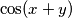
Rješenje zapiši u ovliku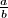 
pri ćemu su 
i 
relativno prosti cijeli brojevi. Kao odgovor na ovo pitanje zapiši 
.
If
what is
?
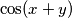
Write the solution in the form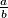 
where 
and 
are relatively prime integers. As the answer to this question, write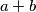 
.
[lang=hr]
Ako
\[
\sin x + \sin y =\frac{1}{2} \quad \cos x - \cos y=\frac{1}{3}
\]
Koliko je $\cos(x+y)$?
Rješenje zapiši u ovliku $\frac{a}{b}$ pri ćemu su $a$ i $b$ relativno prosti cijeli brojevi. Kao odgovor na ovo pitanje zapiši $a+b$.
[/lang]
[lang=en]
If
\[ \sin x + \sin y = \frac{1}{2} \qquad \cos x - \cos y = \frac{1}{3} \]
what is \(\cos(x+y)\)?
Write the solution in the form \(\frac{a}{b}\) where \(a\) and \(b\) are relatively prime integers. As the answer to this question, write \(a+b\).
[/lang]
