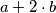Vrijeme: 19:31
From Georgia, with love #3
Postoji  ljudi koji sudjeluju u utrci koja se odvija od jednog grada do drugog. Na startu, svaki trkač (počevši od onog na drugom mjestu) stoji iza drugog trkača. Kažemo da je trkač „dobio poziciju“ ako pretjera samo osobu ispred sebe. Neka je
ljudi koji sudjeluju u utrci koja se odvija od jednog grada do drugog. Na startu, svaki trkač (počevši od onog na drugom mjestu) stoji iza drugog trkača. Kažemo da je trkač „dobio poziciju“ ako pretjera samo osobu ispred sebe. Neka je  vrijednost broja svih mogućih utrka, pri čemu nijedna dva moguća rezultata ne završavaju istim krajnjim ishodom i svaki trkač je dobio najviše jednu poziciju. Pronađite
vrijednost broja svih mogućih utrka, pri čemu nijedna dva moguća rezultata ne završavaju istim krajnjim ishodom i svaki trkač je dobio najviše jednu poziciju. Pronađite  .
.
 ljudi koji sudjeluju u utrci koja se odvija od jednog grada do drugog. Na startu, svaki trkač (počevši od onog na drugom mjestu) stoji iza drugog trkača. Kažemo da je trkač „dobio poziciju“ ako pretjera samo osobu ispred sebe. Neka je
ljudi koji sudjeluju u utrci koja se odvija od jednog grada do drugog. Na startu, svaki trkač (počevši od onog na drugom mjestu) stoji iza drugog trkača. Kažemo da je trkač „dobio poziciju“ ako pretjera samo osobu ispred sebe. Neka je  vrijednost broja svih mogućih utrka, pri čemu nijedna dva moguća rezultata ne završavaju istim krajnjim ishodom i svaki trkač je dobio najviše jednu poziciju. Pronađite
vrijednost broja svih mogućih utrka, pri čemu nijedna dva moguća rezultata ne završavaju istim krajnjim ishodom i svaki trkač je dobio najviše jednu poziciju. Pronađite  .
.Rješenje zapišite u obliku 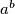 , gdje je
, gdje je  prost broj. Za odgovor na ovo pitanje unesite broj
prost broj. Za odgovor na ovo pitanje unesite broj 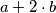 .
.
There are  people participating in a race which takes place from one city to another. At the start, each racer (starting from the one in second position) is standing behind another racer. We say that a racer gained a position if he overtakes only the person in front of him. Let's say that
people participating in a race which takes place from one city to another. At the start, each racer (starting from the one in second position) is standing behind another racer. We say that a racer gained a position if he overtakes only the person in front of him. Let's say that  is the value of number of all possible races, where no two possible races end with the same ending result and each racer only gained only one position. Find
is the value of number of all possible races, where no two possible races end with the same ending result and each racer only gained only one position. Find  .
.
 people participating in a race which takes place from one city to another. At the start, each racer (starting from the one in second position) is standing behind another racer. We say that a racer gained a position if he overtakes only the person in front of him. Let's say that
people participating in a race which takes place from one city to another. At the start, each racer (starting from the one in second position) is standing behind another racer. We say that a racer gained a position if he overtakes only the person in front of him. Let's say that  is the value of number of all possible races, where no two possible races end with the same ending result and each racer only gained only one position. Find
is the value of number of all possible races, where no two possible races end with the same ending result and each racer only gained only one position. Find  .
.Write the solution in the form 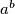 where
where  is a prime. For the answer to this question input the number
is a prime. For the answer to this question input the number