Vrijeme: 19:27
From Georgia, with love #4
Dana je 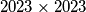 ploča u kojoj su sva polja obojana ili crveno ili crno prema sljedećim pravilima:
ploča u kojoj su sva polja obojana ili crveno ili crno prema sljedećim pravilima: 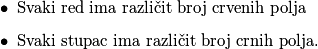 Na koliko različitih načina možemo obojati ploču?
Na koliko različitih načina možemo obojati ploču?
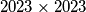 ploča u kojoj su sva polja obojana ili crveno ili crno prema sljedećim pravilima:
ploča u kojoj su sva polja obojana ili crveno ili crno prema sljedećim pravilima: 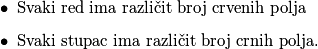 Na koliko različitih načina možemo obojati ploču?
Na koliko različitih načina možemo obojati ploču?Rješenje zapiši u obliku 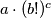 te kao odgovor na ovo pitanje napiši
te kao odgovor na ovo pitanje napiši 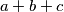
Consider a 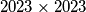 board whose cells are colored either red or black according to the following rules:
board whose cells are colored either red or black according to the following rules:
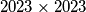 board whose cells are colored either red or black according to the following rules:
board whose cells are colored either red or black according to the following rules:
In how many different ways can the board be colored?
Write the solution in the form 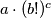 , and as the answer to this question give
, and as the answer to this question give 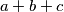 .
.
