Marinada '25

[lang=hr] Ivica je jedan dan sjedio na svojem predavanju iz analize i skužio da lijevo od njega sjedi jedna prekrasna Marica. Marica se Ivici na prvi pogled odmah svidjela, ali joj se nije odmah usudio prići. Kako bi pronašao dobar razlog da joj priđe, Ivica je odlučio pronaći pet "hot" zadataka iz algebre da ju može očarat. 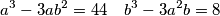Kao prvi takav zadatak, Ivica je smislio: Realni brojevi $a$ i $b$ zadovoljavaju ove jednakosti: \[ a^3-3ab^2=44 \quad b^3-3a^2b=8 \] A vrijednost od 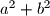$a^2+b^2$ naravno je (rješenje zapiši u obliku $a\sqrt[3]{b}$ pri ćemu je $b$ prost broj, a kao odgovor na ovo pitanje zapiši $a+b$) [/lang] [lang=en] One day, while attending his analysis lecture, Ivica noticed that a beautiful Marica was sitting to his left. He liked her at first sight, but didn’t dare approach her right away. To find a good reason to talk to her, Ivica decided to come up with five “hot” algebra problems that could impress her. As the first such problem, he devised: Real numbers $a$ and $b$ satisfy the equations \[ a^{3}-3ab^{2}=44 \quad b^{3}-3a^{2}b=8 . 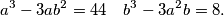\] Find the value of 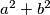$a^{2}+b^{2}$. (Write the answer in the form $a\sqrt[3]{b}$ where $b$ is a prime number, and give the final answer as the sum $a+b$.) [/lang]