Vrijeme: 06:38
Lovegebra #4
Sada su potrebna još dva bomba zadatka, a prvi od tih je:
Niz  zadan je rekurzivno sa
zadan je rekurzivno sa 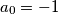

Odredi 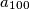 (rješenje zapiši u oliku
(rješenje zapiši u oliku 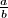 gdje su
gdje su  i
i  relativno prosti cijeli brojevi. Kao odgovor na ovo pitanje napiši
relativno prosti cijeli brojevi. Kao odgovor na ovo pitanje napiši  )
)
Now two more “bomb” problems are required, and the first of them is:
The sequence 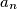 is defined recursively by
is defined recursively by
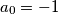

Find 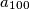 . (Write the solution in the form
. (Write the solution in the form 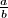 where
where  and
and  are relatively prime integers. As the answer to this question, submit
are relatively prime integers. As the answer to this question, submit  .)
.)
