Vrijeme: 19:27
Lovegebra #5
Za svoj finalni zadatak, Ivica mora biti siguran da će Maricu oborit s nogu. Upravo zato, smislio je najljepši i najteži zadatak do sasd te on glasi ovako:
Neka  bude najveće realno rješenje sljedeće jednadžbe:
bude najveće realno rješenje sljedeće jednadžbe: 
Taj  se može zapisati kao
se može zapisati kao 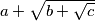 pri ćemu su
pri ćemu su  cijeli brojevi. Koliko je
cijeli brojevi. Koliko je 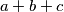 ?
?
For his final assignment, Ivica wants to be absolutely sure that Marica will fall for him. Therefore, he devised the most beautiful and hardest problem ever, which reads as follows:
Let  be the largest real solution of the equation
be the largest real solution of the equation

This number  can be expressed in the form
can be expressed in the form 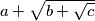 where
where  ,
,  , and
, and  are integers. Find the value of
are integers. Find the value of 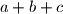 .
.
