Odredi (

je prost)
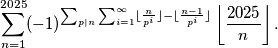
Calculate (

is prime)
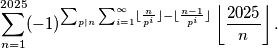
[lang=hr]
Odredi ($p$ je prost)
$$\sum_{n = 1}^{2025} (-1)^{\sum_{p \mid n} \sum_{i = 1}^{\infty} \lfloor \frac{n}{p^i} \rfloor - \lfloor \frac{n - 1}{p^i} \rfloor} \left \lfloor \frac{2025}{n} \right \rfloor.$$
[/lang]
[lang=en]
Calculate ($p$ is prime)
$$\sum_{n = 1}^{2025} (-1)^{\sum_{ p \mid n} \sum_{i = 1}^{\infty} \lfloor \frac{n}{p^i} \rfloor - \lfloor \frac{n - 1}{p^i} \rfloor} \left \lfloor \frac{2025}{n} \right \rfloor.$$
[/lang]