Marinada '25

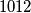[lang=hr] Martin je pozvao Hrvoja na razgovor i rekao mu da je jako bitno da ga dobro sasluša. Hrvoje je odmah uzeo papir i olovku kako bi zapisao Martinove važne riječi. Dok je Martin pričao, Hrvoje je na papiru crtao zvijezde. Konkretno, Hrvoje je s jednakom vjerojatnošću odabrao prirodni broj $s$ od $1$ do $1012$ (uključno). Zatim je nacrtao konveksni 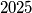$2025$-terokut i u smjeru kazaljke na satu numerirao njegove vrhove od $0$ do $n - 1$. 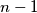Hrvoje kreće iz 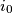$i_0$-tog vrha 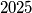$2025$-terokuta i spaja taj vrh s vrhom čiji broj odgovara broju 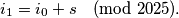\[ i_1 = i_0 + s \pmod{2025}. \] Zatim kreće iz vrha 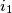$i_1$ i ponavlja taj postupak dok ne dođe do vrha u kojem je već bio. Općenito vrijedi 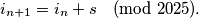\[ i_{n + 1} = i_n + s \pmod{2025}. \] Kolika je vjerojatnost da će proći kroz svih $n$ vrhova, tj. da će se zaustaviti u točki $i_0$. 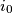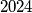\textbf{Napomena:} svi rezultati dobiveni modulom su u rasponu od $0$ do $2024$ (uključno). [/lang] [lang=en] Martin invited Hrvoje for a conversation and told him it was very important that he listen carefully. Hrvoje immediately took a piece of paper and a pencil to write down Martin's important words. While Martin was talking, Hrvoje was drawing stars on the paper. 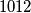Specifically, Hrvoje chose a natural number $s$ uniformly at random from $1$ to $1012$ (inclusive). Then he drew a convex 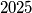$2025$-gon and numbered its vertices clockwise from $0$ to $n - 1$. 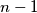Hrvoje starts from vertex 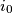$i_0$ of the 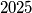$2025$-gon and connects that vertex to the vertex whose number is 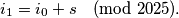\[ i_1 = i_0 + s \pmod{2025}. \] Then, starting from vertex 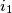$i_1$, he repeats this process until he reaches a vertex he has already visited. In general, it holds that 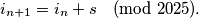\[ i_{n + 1} = i_n + s \pmod{2025}. \] Determine the probability that he will pass through all $n$ vertices, i.e., that he will stop again at the starting vertex $i_0$. 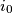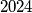\textbf{Note:} All results obtained modulo are in the range from $0$ to $2024$ (inclusive). [/lang]