Vrijeme: 19:27
Vrtićka grupa | Made for children #2
Call a rational number sweet if it has finitely many digits in its decimal expansion. For a positive integer  , we say that a positive integer
, we say that a positive integer  is
is  tastic if there exists a number
tastic if there exists a number 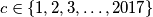 such that
such that 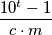 is sweet, and such that
is sweet, and such that 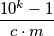 is not sweet for any
is not sweet for any 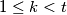 . Let
. Let 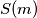 be the set of
be the set of  tastic numbers. Consider
tastic numbers. Consider 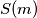 for
for 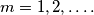 What is the maximum number of elements in
What is the maximum number of elements in 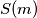 ?
?
 , we say that a positive integer
, we say that a positive integer  is
is  tastic if there exists a number
tastic if there exists a number 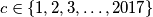 such that
such that 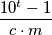 is sweet, and such that
is sweet, and such that 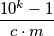 is not sweet for any
is not sweet for any 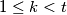 . Let
. Let 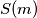 be the set of
be the set of  tastic numbers. Consider
tastic numbers. Consider 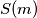 for
for 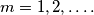 What is the maximum number of elements in
What is the maximum number of elements in 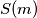 ?
? Nazovimo racionalni broj slatkim ako sadrži konačan broj znamenki u svom decimalnom zapisu. za pozitivni cijeli broj  kažemo da pozitivni cijeli broj
kažemo da pozitivni cijeli broj  je
je  tastičan ako postoji broj
tastičan ako postoji broj 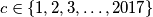 tako da
tako da 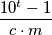 je sladak, i tako da
je sladak, i tako da 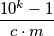 nije sladak za bilo koji
nije sladak za bilo koji 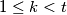 . Neka je
. Neka je 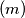 skup svih
skup svih  tastičnih brojeva. Razmotri
tastičnih brojeva. Razmotri 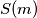 za
za 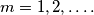 . Koji je maksimalni broj elemenata u
. Koji je maksimalni broj elemenata u 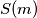 ?
?
 kažemo da pozitivni cijeli broj
kažemo da pozitivni cijeli broj  je
je  tastičan ako postoji broj
tastičan ako postoji broj 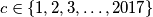 tako da
tako da 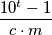 je sladak, i tako da
je sladak, i tako da 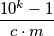 nije sladak za bilo koji
nije sladak za bilo koji 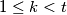 . Neka je
. Neka je 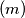 skup svih
skup svih  tastičnih brojeva. Razmotri
tastičnih brojeva. Razmotri 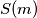 za
za 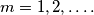 . Koji je maksimalni broj elemenata u
. Koji je maksimalni broj elemenata u 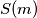 ?
? 