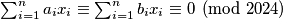Vrijeme: 19:29
Vrtićka grupa | Made for children #3
Find the smallest positive integer  , such that for any integers
, such that for any integers 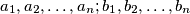 there exists integers
there exists integers 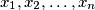 satisfying the following two conditions:
satisfying the following two conditions:
 , such that for any integers
, such that for any integers 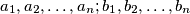 there exists integers
there exists integers 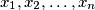 satisfying the following two conditions:
satisfying the following two conditions:i) There exists 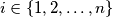 such that
such that 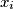 and
and 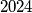 are coprime
are coprime
ii) 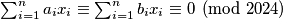
Nađi najmanji cijeli broj  tako da za bilo koje cijele brojeve
tako da za bilo koje cijele brojeve 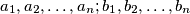 postoje cijeli brojevi
postoje cijeli brojevi 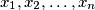 koji zadovoljavaju sljedeća dva uvjeta :
koji zadovoljavaju sljedeća dva uvjeta :
 tako da za bilo koje cijele brojeve
tako da za bilo koje cijele brojeve 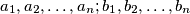 postoje cijeli brojevi
postoje cijeli brojevi 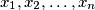 koji zadovoljavaju sljedeća dva uvjeta :
koji zadovoljavaju sljedeća dva uvjeta :1) Postoji 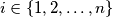 tako da
tako da 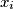 i
i 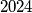 su relativno prosti.
su relativno prosti.
2)