Vrijeme: 19:28
Vrtićka grupa | Made for children #4
Let  ,
,  ,
,  , and
, and  be positive integers with
be positive integers with  and
and  odd. The sequence
odd. The sequence 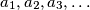 is defined by
is defined by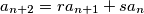 for all
for all 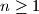 . Determine the maximum possible number of integers
. Determine the maximum possible number of integers 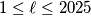 such that
such that 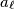 divides
divides 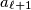 , over all possible choices of
, over all possible choices of  ,
,  ,
,  , and
, and  .
.
 ,
,  ,
,  , and
, and  be positive integers with
be positive integers with  and
and  odd. The sequence
odd. The sequence 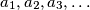 is defined by
is defined by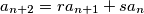 for all
for all 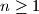 . Determine the maximum possible number of integers
. Determine the maximum possible number of integers 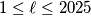 such that
such that 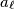 divides
divides 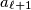 , over all possible choices of
, over all possible choices of  ,
,  ,
,  , and
, and  .
. Neka su  ,
,  ,
,  , i
, i  pozitivni cijeli brojevi i vrijedi
pozitivni cijeli brojevi i vrijedi  i
i  su neparni brojevi. Niz
su neparni brojevi. Niz 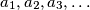 je definiran na sljedeći način:
je definiran na sljedeći način: 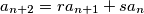 za sve
za sve 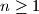 . Odredi maksimalni mogući broj cijelih brojeva
. Odredi maksimalni mogući broj cijelih brojeva 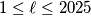 tako da
tako da 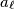 dijeli
dijeli 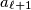 za sve moguće izbore
za sve moguće izbore  ,
,  ,
,  i
i  .
.
 ,
,  ,
,  , i
, i  pozitivni cijeli brojevi i vrijedi
pozitivni cijeli brojevi i vrijedi  i
i  su neparni brojevi. Niz
su neparni brojevi. Niz 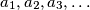 je definiran na sljedeći način:
je definiran na sljedeći način: 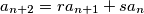 za sve
za sve 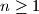 . Odredi maksimalni mogući broj cijelih brojeva
. Odredi maksimalni mogući broj cijelih brojeva 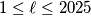 tako da
tako da 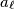 dijeli
dijeli 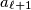 za sve moguće izbore
za sve moguće izbore  ,
,  ,
,  i
i  .
. 