Neka je

polinom s cjelobrojnim koeficijentima takav da je za jedinstvene cijele brojeve
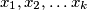
,

Pronađite najveću moguću vrijednost broja  .
.
Let

be a polynomial with integer coefficients such that for distinct integers

it holds that

Find the largest possible value of

.
[lang=hr]
Neka je $P(x)$ polinom s cjelobrojnim koeficijentima takav da je za jedinstvene cijele brojeve $x_1, x_2, \dots x_k$,
$$P(0) = 11 \quad i \quad P(x_1) = P(x_2) = \dots = P(x_k) = 2002$$
Pronađite najveću moguću vrijednost broja $k$.
[/lang]
[lang=en]
Let $P(x)$ be a polynomial with integer coefficients such that for distinct integers $x_1, x_2, \dots, x_k$ it holds that
\[
P(0) = 11 \quad \text{and} \quad P(x_1) = P(x_2) = \dots = P(x_k) = 2002.
\]
Find the largest possible value of $k$.
[/lang]