U nastavku donosim tijek rješavanja mentora (sebe) koji se prvi put susreće s Fikom i njegovim problemima. Izuzetno je korisno da prije čitanja nastavka sami utrošite neko vrijeme na pokušaj rješavanja ovog problema. Uzmite si vremena, rješavajte opušteno, istražujte razne smjerove razmišljanja i isprobajte razne pristupe. Ovaj tjedan neće biti puno zadataka, upravo zato da bi se kvalitetno mogli posvetiti svakom postavljenom problemu i izvući maksimalnu korist iz postupka rješavanja.
With that said, započnimo naše ,,putovanje u središte problema'', kako bi neki glasoviti autori to sročili.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
Prvo jedna benigna napomena. Pišem u prvom licu jednine, što je nekarakteristično za matematički stil, u kojem se uobičajeno piše u prvom licu množine i ponekad u pasivnom obliku (link). Ovim želim naglasiti neposrednost autorskog procesa tijekom rješavanja matematičkog problema. Svako rješenje koje stvaramo malo je autorsko djelo.
Pratit ću Polyine korake, opisane u zadatku Polya - teorija, pa da vidimo gdje će me to odvesti.
Korak 1: Razumijevanje problema.
Nema druge, ako mislimo riješiti problem, prvo ga moramo razumjeti. Inače bismo mogli rješavati krivi problem ili čak riješiti dani problem, a ne biti svjesni toga ;P Prva stvar koju vam preporučam da napravite na početku rješavanja problema jest da ga ... prepišete! Da, dobro ste čuli: uzmete papir i olovku (koje već imate spremne) i prepišete tekst zadatka riječ po riječ. Ovo izgleda kao potpuni gutbitak vremena, ali pomaže nam na najmanje dva načina: dajemo si vremena da još jednom ,,upijemo'' zadatak svojim tempom te nam omogućuje da se potpuno fokusiramo na rješavanje problema, a ne ni na jednu od 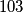 druge stvari koje bismo mogli sada raditi. I nemojte samo prepisivati: razmišljajte o problemu, stvarajte si mentalnu sliku o njemu i pobrinite se da sve razumijete.
druge stvari koje bismo mogli sada raditi. I nemojte samo prepisivati: razmišljajte o problemu, stvarajte si mentalnu sliku o njemu i pobrinite se da sve razumijete.
Dakle, evo za početak tekst zadatka još jednom:
U prostoriji se nalazi  kutija visine
kutija visine  ,
,  ,
,  ,
,  ,
,  koje treba nekim poretkom smjestiti uza zid. Mačak Fiko može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za
koje treba nekim poretkom smjestiti uza zid. Mačak Fiko može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za  viša od one na kojoj se trenutno nalazi. Na koliko načina se kutije mogu poredati tako da Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju?
viša od one na kojoj se trenutno nalazi. Na koliko načina se kutije mogu poredati tako da Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju?
Možda ste tijekom prepisivanja nacrtali i koju sličicu, recimo neki raspored kutija raznih visina, ili ilustraciju Fikovih dozvoljenih skokova. Možda i samog Fika, što je dobra vježba za sat likovnog. Što nas sad može zanimati je pitanje: kako mogu preformulirati dani problem, na način kako bih ga ja napisao?
Meni osobno recimo pada na pamet da malo formaliziramo stvar i uvedemo pojmove dozvoljenog skoka i dobrog rasporeda kutija. Čini mi se da bi to moglo biti korisno dalje u pisanju rješenja. Tekst zadatka bi onda glasio ovako:
U prostoriji se nalazi  kutija visine
kutija visine  ,
,  ,
,  ,
,  ,
,  koje treba nekim poretkom smjestiti uza zid. Mačak Fiko skače po kutijama počevši s prve kutije u nizu. Dozvoljeni skok za Fika je sljedeći: on može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za
koje treba nekim poretkom smjestiti uza zid. Mačak Fiko skače po kutijama počevši s prve kutije u nizu. Dozvoljeni skok za Fika je sljedeći: on može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za  viša od one na kojoj se trenutno nalazi. Raspored kutija zovemo dobrim ako Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju, koristeći pritom samo dozvoljene skokove. Pitanje je sada: koliko postoji dobrih rasporeda?
viša od one na kojoj se trenutno nalazi. Raspored kutija zovemo dobrim ako Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju, koristeći pritom samo dozvoljene skokove. Pitanje je sada: koliko postoji dobrih rasporeda?
Istina, s ovim nismo ništa bliže rješenju problema, ali ne brinite još oko toga. Za sada se samo bavimo razumijevanjem samog problema. Primjetimo ipak kako nakon ove male preformulacije stil problema postaje ,,ozbiljniji'', sličniji nečemu s čime biste se susreli na nekom ,,ozbiljnom'' natjecanju.
Sada bismo već trebali biti u poziciji da odgovorimo na Polyina pitanja vezana uz prvi korak. Evo mojih pokušaja.
Što je nepoznato? - Broj dobrih rasporeda.
Što su poznati podaci - Broj i visina kutija, činjenica da ih slažemo jednu do druge nekim redom i pojmovi Fikovog dozvoljenog skoka i dobrog rasporeda kutija.
Jesu li zadani uvjeti dovoljni da se odredi nepoznato? - Da. Svakako nisu kontradiktorni: trivijalni raspored kutija po rastućoj visini je očito jedan dobar raspored. Nadalje, za svaki mogući raspored kutija jednoznačno možemo odrediti je li dobar ili ne. Stoga smo u poziciji da od svih rasporeda odredimo dobre i prebrojimo ih.
Toliko o razumijevanju problema. Napokon, okrećem se pokušajima rješavanja.
Korak 2: Smišljanje plana.
OK, znači zanimaju nas dobri rasporedi. Jedan raspored može se ustvari shvatiti kao permutacija skupa brojeva 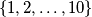 , pod uvjetom da kutije nazovemo redom brojevima
, pod uvjetom da kutije nazovemo redom brojevima  ,
,  ,
,  ,
,  . Dodatno, učinimo to na prirodan način: neka je kutija broj
. Dodatno, učinimo to na prirodan način: neka je kutija broj  visine
visine  , kutija broj
, kutija broj  visine
visine  , itd. do kutije broj
, itd. do kutije broj  . Permutacija inače nije ništa drugo doli uređeni (=,,u redu'') raspored nekih objekata.
. Permutacija inače nije ništa drugo doli uređeni (=,,u redu'') raspored nekih objekata.
Sad se pitamo koliko uopće postoji permutacija skupa 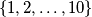 . Odgovor na ovo pitanje lijepo je objašnjen ovdje. Dakle, ukupno postoji
. Odgovor na ovo pitanje lijepo je objašnjen ovdje. Dakle, ukupno postoji 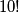 različitih permutacija, što je blago rečeno nezanemariv broj. Ovime smo ograničili broj dobrih permutacija na raspon
različitih permutacija, što je blago rečeno nezanemariv broj. Ovime smo ograničili broj dobrih permutacija na raspon  -
- 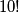 . Nije nešto, ali tek je početak. I barem smo uvjereni da ćemo ovaj zadatak teško riješiti ,,na prste''.
. Nije nešto, ali tek je početak. I barem smo uvjereni da ćemo ovaj zadatak teško riješiti ,,na prste''.
Mogu li za početak nekako pojednostaviti problem? Svakako, upravo smo rješavali pojednostavljenu varijantu ovog problema, sa samo  kutije. Krećem i ja tim putem.
kutije. Krećem i ja tim putem.
Označimo dakle broj kutija s  .
.
Za  , zadatak praktički ne postoji: jedina moguća permutacija je trivijalno dobra. Za
, zadatak praktički ne postoji: jedina moguća permutacija je trivijalno dobra. Za  , problem ostaje trivijalan, ali počinju bar neke kombinacije: obje moguće permutacije
, problem ostaje trivijalan, ali počinju bar neke kombinacije: obje moguće permutacije 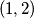 i
i 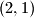 su dobre. Za
su dobre. Za 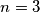 , od mogućih
, od mogućih  permutacija, vidim da
permutacija, vidim da  čine dobar raspored:
čine dobar raspored: 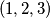 ,
, 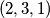 ,
, 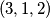 ,
, 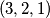 . Za
. Za 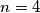 , već postoji
, već postoji 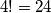 moguće permutacije. Od toga, sljedeće su dobre:
moguće permutacije. Od toga, sljedeće su dobre: 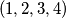 ,
, 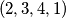 ,
, 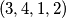 ,
,  ,
, 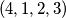 ,
, 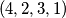 ,
, 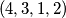 ,
, 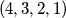 ; dakle
; dakle  ukupno. Uvjerite se sami da su napisani odgovori doista ispravni - nikad ne vjerujte slijepo autoru (pa ni meni)!
ukupno. Uvjerite se sami da su napisani odgovori doista ispravni - nikad ne vjerujte slijepo autoru (pa ni meni)!
Hm hm,  ,
,  ,
,  ,
,  -> nešto tu smrdi, i to na potencije broja
-> nešto tu smrdi, i to na potencije broja  ! Zašto, kako? Dobro, da se ne pravim lud previše, priznajem da sam između zadnjih redaka shvatio što se događa i došao do konačnog rješenja, kao možda i neki od vas. Idem sad probati opisati taj proces.
! Zašto, kako? Dobro, da se ne pravim lud previše, priznajem da sam između zadnjih redaka shvatio što se događa i došao do konačnog rješenja, kao možda i neki od vas. Idem sad probati opisati taj proces.
Gledam što se događa na prijelazu između  i
i  . Prva opservacija je sljedeća: jedina novost između tri i četiri kutije je (očito) četvrta kutija visine
. Prva opservacija je sljedeća: jedina novost između tri i četiri kutije je (očito) četvrta kutija visine  . Prve tri kutije iz nekog dobrog rasporeda moraju ostati u istom međusobnom položaju kao i dok su bile samo tri, jer se dodavanjem četvrte ništa nije promijenilo ,,što se njih tiče''. Dakle, možemo početi od
. Prve tri kutije iz nekog dobrog rasporeda moraju ostati u istom međusobnom položaju kao i dok su bile samo tri, jer se dodavanjem četvrte ništa nije promijenilo ,,što se njih tiče''. Dakle, možemo početi od  dobra rasporeda koja imamo za slučaj s
dobra rasporeda koja imamo za slučaj s  kutije i pitati se gdje možemo ,,umetnuti" četvrtu kutiju.
kutije i pitati se gdje možemo ,,umetnuti" četvrtu kutiju.
Uzmem prvo dobru permutaciju 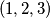 . Kutiju visine
. Kutiju visine  mogu staviti na početak, jer Fiko sa svojih
mogu staviti na početak, jer Fiko sa svojih  mačjih života može podnijeti skok prema dolje s bilo koje visine. Gdje još? Ne mogu iza
mačjih života može podnijeti skok prema dolje s bilo koje visine. Gdje još? Ne mogu iza  , to mu je previsoko. Isto tako i iza
, to mu je previsoko. Isto tako i iza  . Jedino može doći na kraj iza
. Jedino može doći na kraj iza  . Time od jednog dobrog rasporeda za
. Time od jednog dobrog rasporeda za 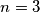 dobijem dva dobra rasporeda za
dobijem dva dobra rasporeda za 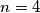 .
.
Gledam sada sljedeću dobru permutaciju 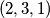 . Ponovno, kutiju
. Ponovno, kutiju  mogu staviti na početak, a osim toga opet jedino iza kutije
mogu staviti na početak, a osim toga opet jedino iza kutije  . Primjećujem da nakon što je umetnem tako između
. Primjećujem da nakon što je umetnem tako između  i
i  , nisam ništa ,,pokvario'', ponovno jer su dozvoljeni skokovi prema dolje s bilo koje visine. Dakle, i u ovom slučaju od jedne dobre permutacije za
, nisam ništa ,,pokvario'', ponovno jer su dozvoljeni skokovi prema dolje s bilo koje visine. Dakle, i u ovom slučaju od jedne dobre permutacije za 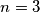 dobivam dvije dobre permutacije za
dobivam dvije dobre permutacije za 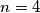 .
.
Pattern emerges, ilitiga: AHA! Imam ga! Slutimo da će se broj dobrih permutacija duplo povećavati sa svakim povećanjem broja kutija  za jedan. Plan je smišljen, pokušajmo ga provesti!
za jedan. Plan je smišljen, pokušajmo ga provesti!
Korak 3: Provedba plana.
Još je Arhimed rekao: ,,Daj mi dobar plan i riješit ću ti problem.'' Ili nešto tako. Da vidimo je li bio u pravu.
Neka je 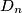 broj dobrih rasporeda s
broj dobrih rasporeda s  kutija. Želimo odrediti broj dobrih permutacija
kutija. Želimo odrediti broj dobrih permutacija 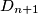 za
za  kutiju, u ovisnosti o
kutiju, u ovisnosti o 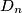 .
.
Uzmimo dakle proizvoljan dobar raspored (bilo koji od 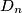 mogućih) za
mogućih) za  kutija. Označimo ga s
kutija. Označimo ga s 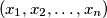 , gdje su jasno
, gdje su jasno  međusobno različiti elementi skupa
međusobno različiti elementi skupa 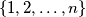 koji predstavljaju redni broj (ujedno i visinu) kutije. Sad se pitamo kako od ovog rasporeda možemo napraviti dobar raspored za
koji predstavljaju redni broj (ujedno i visinu) kutije. Sad se pitamo kako od ovog rasporeda možemo napraviti dobar raspored za  kutiju. Kao što smo prije zaključili, jedina stvar koju moramo napraviti je vidjeti gdje možemo ,,ubaciti'' kutiju
kutiju. Kao što smo prije zaključili, jedina stvar koju moramo napraviti je vidjeti gdje možemo ,,ubaciti'' kutiju  . Ponovno kao prije, vidimo da je sigurno možemo ubaciti na sami početak niza. Time dobivamo dobar raspored
. Ponovno kao prije, vidimo da je sigurno možemo ubaciti na sami početak niza. Time dobivamo dobar raspored 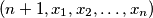 za
za  kutiju.
kutiju.
Pitamo se gdje još možemo ubaciti kutiju  . Sad neće biti na početku, što znači da će biti neka kutija ispred nje. To je ključ: da bi Fiko došao na kutiju
. Sad neće biti na početku, što znači da će biti neka kutija ispred nje. To je ključ: da bi Fiko došao na kutiju  dozvoljenim skokom, jedina mogućnost je da prije nje bude na kutiji
dozvoljenim skokom, jedina mogućnost je da prije nje bude na kutiji  , jer je to jedina manja s koje se može popeti na
, jer je to jedina manja s koje se može popeti na  , a više kutije od
, a više kutije od  nema. Dakle, ako je
nema. Dakle, ako je  takav da
takav da 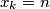 , još jedan dobar raspored za
, još jedan dobar raspored za  kutiju je
kutiju je 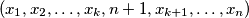 .
.
Zaključak je tu: od jednog, proizvoljnog, dobrog rasporeda za  kutija, dobivamo točno dva dobra rasporeda za
kutija, dobivamo točno dva dobra rasporeda za  kutiju. Možemo li zaključiti da vrijedi
kutiju. Možemo li zaključiti da vrijedi 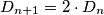 ? Skoro, ostaje dokazati da svi dobri rasporedi za
? Skoro, ostaje dokazati da svi dobri rasporedi za  kutiju moraju nastati upravo na ovaj način. Ali to nije teško i možda smo implicitno već dokazali u prijašnjoj raspravi, ostavljam vam za zadaću (HINT: uzme se proizvoljni raspored za
kutiju moraju nastati upravo na ovaj način. Ali to nije teško i možda smo implicitno već dokazali u prijašnjoj raspravi, ostavljam vam za zadaću (HINT: uzme se proizvoljni raspored za  kutiju i ,,izbriše'' se kutija
kutiju i ,,izbriše'' se kutija  : treba dokazati da je to dobar raspored za
: treba dokazati da je to dobar raspored za  kutija).
kutija).
Sada, konačno je dokazano 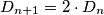 . Krasno! Ostaje riješiti ovu rekurziju. Rekurzije znaju biti zeznute, upravo zato što rekurzije znaju biti zeznute. Ali srećom, ova naša je ,,pitoma''. Početna vrijednost je
. Krasno! Ostaje riješiti ovu rekurziju. Rekurzije znaju biti zeznute, upravo zato što rekurzije znaju biti zeznute. Ali srećom, ova naša je ,,pitoma''. Početna vrijednost je 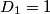 . Za
. Za 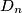 lako možemo razmotati:
lako možemo razmotati: 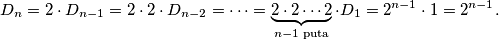
Voila,  , za sve
, za sve  (uklapa se čak i za polaznu vrijednost
(uklapa se čak i za polaznu vrijednost  ). Riješeno! Ostaje se vratiti na konkretno pitanje iz zadatka --- to ostavljam vama; kao rješenje prethodnog zadatka upišite dobivenu vrijednost.
). Riješeno! Ostaje se vratiti na konkretno pitanje iz zadatka --- to ostavljam vama; kao rješenje prethodnog zadatka upišite dobivenu vrijednost.
Korak 4: Osvrt.
Često, prečesto zanemarivan korak. Priznajem, i ja sam u vašim godinama premalo vremena trošio na naknadno razmatranje rjiešenog zadatka. Ali i kratki osvrt može biti jako koristan. Samo prođite još jednom kroz sve korake svog konačnog rješenja i uvjerite se da sve razumijete i da ćete moći bez poteškoća riješiti slične probleme u budućnosti. Time prvo izbjegvate male i glupe greške napravljene u žaru postupka rješavanja te dodatno osnažujete svoje znanje o temi zadatka.
Kad prođem kratko kroz rješenje, prvo mi se sviđa uvođenje pojmova dozvoljenog skoka i posebice dobrog rasporeda, jer su mi olakšali komunikaciju i razmišljanje o problemu. Potvrđujem činjenicu da je promatranje jednostavnijih problema često put prema rješavanju onih koji se ispočetka čine prekomplicirani. Ostalo mi je sve u redu, svjedočim još jednom da je rekurzivno ili induktivno razmišljanje jako efektivna matematička metoda, pogotovo u kombinatorici.
Nadalje, evo još jedna skrivena korist od osvrta. Osobno, još i sada kao mentoru (s ograničenim iskustvom) mi još nije uvijek jasno kako se netko dosjeti postaviti ovakav zadatak. Mislim da je najbolji način za to osvrtanje na problem nakon što smo našli rješenje, i to iz perspektive nekoga sada ,,ravnog zadatku'', a ne više podređenog i pod teretom traženja rješenja. Sada se možemo pitati kako je autor uopće došao do ideje za zadatak. Možemo se staviti u njegovu kožu i malo se igrati s uvjetima, pokušati neke izmijeniti, napraviti sličan zadatak i vdjeti kako se rješenje mijenja u ovisnosti o tim parametrima. Recimo, ovaj zadatak je idealan za takve mentalne egzibicije. Što ako kutije nisu visina  ,
,  ,
,  ,
,  , nego nekih drugih? Što ako promijenimo Fikove sposobnosti skakanja uvis ili dolje? Ili još egzotičnije, što ako postoji više redova kutija, a ne samo jedan, pa pustimo Fika neka može skakati s reda na red? Što ako uključimo i Fikovu braću i sestre koji se isto žele igrati skakanja po kutijama? Samo je nebo granica i vaša mašta. Predlažem da svatko od vas smisli jednu varijantu Fikovog problema. Šaljite nam svoje zadatke i možda neke i uvrstimo u idući MetaMath!
, nego nekih drugih? Što ako promijenimo Fikove sposobnosti skakanja uvis ili dolje? Ili još egzotičnije, što ako postoji više redova kutija, a ne samo jedan, pa pustimo Fika neka može skakati s reda na red? Što ako uključimo i Fikovu braću i sestre koji se isto žele igrati skakanja po kutijama? Samo je nebo granica i vaša mašta. Predlažem da svatko od vas smisli jednu varijantu Fikovog problema. Šaljite nam svoje zadatke i možda neke i uvrstimo u idući MetaMath!
Još par napomena u sklopu osvrta na proces rješavanja. Ovaj zadatak je prilično jednostavan i zbog toga smo imali sreću da odmah iz prve postavimo dobru slutnju i krenemo pravim putem prema rješenju. No, sami znate da to nije uvijek slučaj u tijeku rješavanja problema. Često krenemo krivim putem koji ne vodi nužno rješenju, barem ne na najelegantniji način. Recimo, ovdje smo mogli ići brojati dobre rasporede metodama klasičnog prebrojavanja, principom sume i uzastopnog prebrojavanja. Možda je moguće ići i tim putem, ali vjerojatno manje u pravoj liniji kao u ovom rješenju. U svakom slučaju, isprobajte svaki put koji vam padne na pamet, do neke dubine. Time ćete stvoriti osjećaj za raspoznavanje dobrog puta od pogrešnog i razviti sposobnost samokritičnosti i samoprocjene. Najvažnije od svega, cijenite cjelokupni proces rješavanja, sve uspone i padove, slijepe ulice i stranputice, jer je moguće da ćete više naučiti iz njih nego od čitanja nečijeg već napisanog rješenja.
Kao rješenje upišite ,,Fiko''.
U nastavku donosim tijek rješavanja mentora (sebe) koji se prvi put susreće s Fikom i njegovim problemima. Izuzetno je korisno da prije čitanja nastavka \emph{sami utrošite neko vrijeme na pokušaj rješavanja ovog problema}. Uzmite si vremena, rješavajte opušteno, istražujte razne smjerove razmišljanja i isprobajte razne pristupe. Ovaj tjedan neće biti puno zadataka, upravo zato da bi se kvalitetno mogli posvetiti svakom postavljenom problemu i izvući maksimalnu korist iz postupka rješavanja.
With that said, započnimo naše ,,putovanje u središte problema'', kako bi neki glasoviti autori to sročili.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
Prvo jedna benigna napomena. Pišem u prvom licu jednine, što je nekarakteristično za matematički stil, u kojem se uobičajeno piše u prvom licu množine i ponekad u pasivnom obliku (\href{https://math.stackexchange.com/questions/604277/why-are-proofs-written-in-first-person-plural-were-they-ever-written-differentl}{link}). Ovim želim naglasiti neposrednost autorskog procesa tijekom rješavanja matematičkog problema. Svako rješenje koje stvaramo malo je autorsko djelo.
Pratit ću Polyine korake, opisane u zadatku \href{https://www.skoljka.org/metamath23/task/2191/}{Polya - teorija}, pa da vidimo gdje će me to odvesti.
\textbf{Korak 1: Razumijevanje problema.}
Nema druge, ako mislimo riješiti problem, prvo ga moramo razumjeti. Inače bismo mogli rješavati krivi problem ili čak riješiti dani problem, a ne biti svjesni toga ;P Prva stvar koju vam preporučam da napravite na početku rješavanja problema jest da ga ... \emph{prepišete}! Da, dobro ste čuli: uzmete papir i olovku (koje već imate spremne) i prepišete tekst zadatka riječ po riječ. Ovo izgleda kao potpuni gutbitak vremena, ali pomaže nam na najmanje dva načina: dajemo si vremena da još jednom ,,upijemo'' zadatak svojim tempom te nam omogućuje da se potpuno fokusiramo na rješavanje problema, a ne ni na jednu od $103$ druge stvari koje bismo mogli sada raditi. I nemojte samo prepisivati: razmišljajte o problemu, stvarajte si mentalnu sliku o njemu i pobrinite se da sve razumijete.
Dakle, evo za početak tekst zadatka još jednom:\\
U prostoriji se nalazi $10$ kutija visine $1$, $2$, $3$, $\dots$, $10$ koje treba nekim poretkom smjestiti uza zid. Mačak Fiko može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za $1$ viša od one na kojoj se trenutno nalazi. Na koliko načina se kutije mogu poredati tako da Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju?
Možda ste tijekom prepisivanja nacrtali i koju sličicu, recimo neki raspored kutija raznih visina, ili ilustraciju Fikovih dozvoljenih skokova. Možda i samog Fika, što je dobra vježba za sat likovnog. Što nas sad može zanimati je pitanje: kako mogu preformulirati dani problem, na način kako bih ga ja napisao?
Meni osobno recimo pada na pamet da malo formaliziramo stvar i uvedemo pojmove \emph{dozvoljenog skoka} i \emph{dobrog rasporeda kutija}. Čini mi se da bi to moglo biti korisno dalje u pisanju rješenja. Tekst zadatka bi onda glasio ovako:
U prostoriji se nalazi $10$ kutija visine $1$, $2$, $3$, $\dots$, $10$ koje treba nekim poretkom smjestiti uza zid. Mačak Fiko skače po kutijama počevši s prve kutije u nizu. \emph{Dozvoljeni skok} za Fika je sljedeći: on može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za $1$ viša od one na kojoj se trenutno nalazi. Raspored kutija zovemo \emph{dobrim} ako Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju, koristeći pritom samo dozvoljene skokove. Pitanje je sada: koliko postoji dobrih rasporeda?
Istina, s ovim nismo ništa bliže rješenju problema, ali ne brinite još oko toga. Za sada se samo bavimo razumijevanjem samog problema. Primjetimo ipak kako nakon ove male preformulacije stil problema postaje ,,ozbiljniji'', sličniji nečemu s čime biste se susreli na nekom ,,ozbiljnom'' natjecanju.
Sada bismo već trebali biti u poziciji da odgovorimo na Polyina pitanja vezana uz prvi korak. Evo mojih pokušaja.\\
\textit{Što je nepoznato?} - Broj dobrih rasporeda.\\
\textit{Što su poznati podaci} - Broj i visina kutija, činjenica da ih slažemo jednu do druge nekim redom i pojmovi Fikovog dozvoljenog skoka i dobrog rasporeda kutija.\\
\textit{Jesu li zadani uvjeti dovoljni da se odredi nepoznato?} - Da. Svakako nisu kontradiktorni: trivijalni raspored kutija po rastućoj visini je očito jedan dobar raspored. Nadalje, za svaki mogući raspored kutija jednoznačno možemo odrediti je li dobar ili ne. Stoga smo u poziciji da od svih rasporeda odredimo dobre i prebrojimo ih.
Toliko o razumijevanju problema. Napokon, okrećem se pokušajima rješavanja.
\textbf{Korak 2: Smišljanje plana.}
OK, znači zanimaju nas dobri \emph{rasporedi}. Jedan raspored može se ustvari shvatiti kao \emph{permutacija} skupa brojeva $\{1, 2, \dots, 10\}$, pod uvjetom da kutije nazovemo redom brojevima $1$, $2$, $\dots$, $10$. Dodatno, učinimo to na prirodan način: neka je kutija broj $1$ visine $1$, kutija broj $2$ visine $2$, itd. do kutije broj $10$. Permutacija inače nije ništa drugo doli uređeni (=,,u redu'') raspored nekih objekata.
Sad se pitamo koliko uopće postoji permutacija skupa $\{1, 2, \dots, 10\}$. Odgovor na ovo pitanje lijepo je objašnjen \href{https://www.skoljka.org/folder/600/vekijeva-vesela-vjezbenica/predavanja-za-prve-razrede/prebrojavanja/}{ovdje}. Dakle, ukupno postoji $10!$ različitih permutacija, što je blago rečeno nezanemariv broj. Ovime smo ograničili broj dobrih permutacija na raspon $1$ - $10!$. Nije nešto, ali tek je početak. I barem smo uvjereni da ćemo ovaj zadatak teško riješiti ,,na prste''.
Mogu li za početak nekako pojednostaviti problem? Svakako, upravo smo rješavali pojednostavljenu varijantu ovog problema, sa samo $3$ kutije. Krećem i ja tim putem.
Označimo dakle broj kutija s $n$.\\
Za $n=1$, zadatak praktički ne postoji: jedina moguća permutacija je trivijalno dobra. Za $n=2$, problem ostaje trivijalan, ali počinju bar neke kombinacije: obje moguće permutacije $(1, 2)$ i $(2, 1)$ su dobre. Za $n=3$, od mogućih $6$ permutacija, vidim da $4$ čine dobar raspored: $(1, 2, 3)$, $(2, 3, 1)$, $(3, 1, 2)$, $(3, 2, 1)$. Za $n=4$, već postoji $4!=24$ moguće permutacije. Od toga, sljedeće su dobre: $(1, 2, 3, 4)$, $(2, 3, 4, 1)$, $(3, 4, 1, 2)$, $(3, 4, 2, 1)$, $(4, 1, 2, 3)$, $(4, 2, 3, 1)$, $(4, 3, 1, 2)$, $(4, 3, 2, 1)$; dakle $8$ ukupno. Uvjerite se sami da su napisani odgovori doista ispravni - nikad ne vjerujte slijepo autoru (pa ni meni)!
Hm hm, $1$, $2$, $4$, $8$ -> nešto tu smrdi, i to na potencije broja $2$! Zašto, kako? Dobro, da se ne pravim lud previše, priznajem da sam između zadnjih redaka shvatio što se događa i došao do konačnog rješenja, kao možda i neki od vas. Idem sad probati opisati taj proces.
Gledam što se događa na prijelazu između $3$ i $4$. Prva opservacija je sljedeća: jedina novost između tri i četiri kutije je (očito) četvrta kutija visine $4$. Prve tri kutije iz nekog dobrog rasporeda moraju ostati u istom međusobnom položaju kao i dok su bile samo tri, jer se dodavanjem četvrte ništa nije promijenilo ,,što se njih tiče''. Dakle, možemo početi od $4$ dobra rasporeda koja imamo za slučaj s $3$ kutije i pitati se gdje možemo ,,umetnuti" četvrtu kutiju.
Uzmem prvo dobru permutaciju $(1, 2, 3)$. Kutiju visine $4$ mogu staviti na početak, jer Fiko sa svojih $9$ mačjih života može podnijeti skok prema dolje s bilo koje visine. Gdje još? Ne mogu iza $1$, to mu je previsoko. Isto tako i iza $2$. Jedino može doći na kraj iza $3$. Time od jednog dobrog rasporeda za $n=3$ dobijem dva dobra rasporeda za $n=4$.
Gledam sada sljedeću dobru permutaciju $(2, 3, 1)$. Ponovno, kutiju $4$ mogu staviti na početak, a osim toga opet jedino iza kutije $3$. Primjećujem da nakon što je umetnem tako između $3$ i $1$, nisam ništa ,,pokvario'', ponovno jer su dozvoljeni skokovi prema dolje s bilo koje visine. Dakle, i u ovom slučaju od jedne dobre permutacije za $n=3$ dobivam dvije dobre permutacije za $n=4$.
Pattern emerges, ilitiga: \textbf{AHA!} Imam ga! Slutimo da će se broj dobrih permutacija duplo povećavati sa svakim povećanjem broja kutija $n$ za jedan. Plan je smišljen, pokušajmo ga provesti!
\textbf{Korak 3: Provedba plana.}
Još je Arhimed rekao: ,,Daj mi dobar plan i riješit ću ti problem.'' Ili nešto tako. Da vidimo je li bio u pravu.
Neka je $D_n$ broj dobrih rasporeda s $n$ kutija. Želimo odrediti broj dobrih permutacija $D_{n+1}$ za $n+1$ kutiju, u ovisnosti o $D_n$.
Uzmimo dakle proizvoljan dobar raspored (bilo koji od $D_n$ mogućih) za $n$ kutija. Označimo ga s $(x_1, x_2, \dots, x_n)$, gdje su jasno $x_1, x_2, \dots, x_n$ međusobno različiti elementi skupa $\{ 1, 2, \dots, n \}$ koji predstavljaju redni broj (ujedno i visinu) kutije. Sad se pitamo kako od ovog rasporeda možemo napraviti dobar raspored za $n+1$ kutiju. Kao što smo prije zaključili, jedina stvar koju moramo napraviti je vidjeti gdje možemo ,,ubaciti'' kutiju $n+1$. Ponovno kao prije, vidimo da je sigurno možemo ubaciti na sami početak niza. Time dobivamo dobar raspored $(n+1, x_1, x_2, \dots, x_n)$ za $n+1$ kutiju.
Pitamo se gdje još možemo ubaciti kutiju $n+1$. Sad neće biti na početku, što znači da će biti neka kutija ispred nje. To je ključ: da bi Fiko došao na kutiju $n+1$ dozvoljenim skokom, \emph{jedina mogućnost} je da prije nje bude na kutiji $n$, jer je to jedina manja s koje se može popeti na $n+1$, a više kutije od $n+1$ nema. Dakle, ako je $k$ takav da $x_k=n$, još jedan dobar raspored za $n+1$ kutiju je $(x_1, x_2, \dots, x_k, n+1, x_{k+1}, \dots, x_n)$.
Zaključak je tu: od jednog, proizvoljnog, dobrog rasporeda za $n$ kutija, dobivamo točno dva dobra rasporeda za $n+1$ kutiju. Možemo li zaključiti da vrijedi $D_{n+1} = 2 \cdot D_n$? Skoro, ostaje dokazati da svi dobri rasporedi za $n+1$ kutiju moraju nastati upravo na ovaj način. Ali to nije teško i možda smo implicitno već dokazali u prijašnjoj raspravi, ostavljam vam za zadaću (HINT: uzme se proizvoljni raspored za $n+1$ kutiju i ,,izbriše'' se kutija $n+1$: treba dokazati da je to dobar raspored za $n$ kutija).
Sada, konačno je dokazano $D_{n+1} = 2 \cdot D_n$. Krasno! Ostaje riješiti ovu \href{https://hrcak.srce.hr/file/266709}{rekurziju}. Rekurzije znaju biti zeznute, upravo zato što rekurzije znaju biti zeznute. Ali srećom, ova naša je ,,pitoma''. Početna vrijednost je $D_1 = 1$. Za $D_n$ lako možemo razmotati:
$$ D_n = 2 \cdot D_{n-1} = 2 \cdot 2 \cdot D_{n-2} = \dotsb = \underbrace{2 \cdot 2 \dotsb 2}_{n -1 \text{ puta}} \cdot D_1 = 2^{n-1} \cdot 1 = 2^{n-1}.$$
Voila, $D_n=2^{n-1}$, za sve $n \in \mathbb{N}$ (uklapa se čak i za polaznu vrijednost $n=1$). Riješeno! Ostaje se vratiti na konkretno pitanje iz zadatka --- to ostavljam vama; kao rješenje prethodnog zadatka upišite dobivenu vrijednost.
\textbf{Korak 4: Osvrt.}
Često, prečesto zanemarivan korak. Priznajem, i ja sam u vašim godinama premalo vremena trošio na naknadno razmatranje rjiešenog zadatka. Ali i kratki osvrt može biti jako koristan. Samo prođite još jednom kroz sve korake svog konačnog rješenja i uvjerite se da sve razumijete i da ćete moći bez poteškoća riješiti slične probleme u budućnosti. Time prvo izbjegvate male i glupe greške napravljene u žaru postupka rješavanja te dodatno osnažujete svoje znanje o temi zadatka.
Kad prođem kratko kroz rješenje, prvo mi se sviđa uvođenje pojmova dozvoljenog skoka i posebice dobrog rasporeda, jer su mi olakšali komunikaciju i razmišljanje o problemu. Potvrđujem činjenicu da je promatranje jednostavnijih problema često put prema rješavanju onih koji se ispočetka čine prekomplicirani. Ostalo mi je sve u redu, svjedočim još jednom da je rekurzivno ili induktivno razmišljanje jako efektivna matematička metoda, pogotovo u kombinatorici.
Nadalje, evo još jedna skrivena korist od osvrta. Osobno, još i sada kao mentoru (s ograničenim iskustvom) mi još nije uvijek jasno kako se netko dosjeti postaviti ovakav zadatak. Mislim da je najbolji način za to osvrtanje na problem nakon što smo našli rješenje, i to iz perspektive nekoga sada ,,ravnog zadatku'', a ne više podređenog i pod teretom traženja rješenja. Sada se možemo pitati kako je autor uopće došao do ideje za zadatak. Možemo se staviti u njegovu kožu i malo se igrati s uvjetima, pokušati neke izmijeniti, napraviti sličan zadatak i vdjeti kako se rješenje mijenja u ovisnosti o tim parametrima. Recimo, ovaj zadatak je idealan za takve mentalne egzibicije. Što ako kutije nisu visina $1$, $2$, $\dots$, $n$, nego nekih drugih? Što ako promijenimo Fikove sposobnosti skakanja uvis ili dolje? Ili još egzotičnije, što ako postoji više redova kutija, a ne samo jedan, pa pustimo Fika neka može skakati s reda na red? Što ako uključimo i Fikovu braću i sestre koji se isto žele igrati skakanja po kutijama? Samo je nebo granica i vaša mašta. Predlažem da svatko od vas smisli jednu varijantu Fikovog problema. Šaljite nam svoje zadatke i možda neke i uvrstimo u idući MetaMath!
Još par napomena u sklopu osvrta na proces rješavanja. Ovaj zadatak je prilično jednostavan i zbog toga smo imali sreću da odmah iz prve postavimo dobru slutnju i krenemo pravim putem prema rješenju. No, sami znate da to nije uvijek slučaj u tijeku rješavanja problema. Često krenemo krivim putem koji ne vodi nužno rješenju, barem ne na najelegantniji način. Recimo, ovdje smo mogli ići brojati dobre rasporede metodama klasičnog prebrojavanja, principom sume i uzastopnog prebrojavanja. Možda je moguće ići i tim putem, ali vjerojatno manje u pravoj liniji kao u ovom rješenju. U svakom slučaju, isprobajte svaki put koji vam padne na pamet, do neke dubine. Time ćete stvoriti osjećaj za raspoznavanje dobrog puta od pogrešnog i razviti sposobnost samokritičnosti i samoprocjene. Najvažnije od svega, cijenite cjelokupni proces rješavanja, sve uspone i padove, slijepe ulice i stranputice, jer je moguće da ćete više naučiti iz njih nego od čitanja nečijeg već napisanog rješenja.
\emph{Kao rješenje upišite ,,Fiko''.}
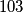 druge stvari koje bismo mogli sada raditi. I nemojte samo prepisivati: razmišljajte o problemu, stvarajte si mentalnu sliku o njemu i pobrinite se da sve razumijete.
druge stvari koje bismo mogli sada raditi. I nemojte samo prepisivati: razmišljajte o problemu, stvarajte si mentalnu sliku o njemu i pobrinite se da sve razumijete. kutija visine
kutija visine  ,
,  ,
,  ,
,  ,
,  koje treba nekim poretkom smjestiti uza zid. Mačak Fiko može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za
koje treba nekim poretkom smjestiti uza zid. Mačak Fiko može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za  viša od one na kojoj se trenutno nalazi. Na koliko načina se kutije mogu poredati tako da Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju?
viša od one na kojoj se trenutno nalazi. Na koliko načina se kutije mogu poredati tako da Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju? kutija visine
kutija visine  ,
,  ,
,  ,
,  ,
,  koje treba nekim poretkom smjestiti uza zid. Mačak Fiko skače po kutijama počevši s prve kutije u nizu. Dozvoljeni skok za Fika je sljedeći: on može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za
koje treba nekim poretkom smjestiti uza zid. Mačak Fiko skače po kutijama počevši s prve kutije u nizu. Dozvoljeni skok za Fika je sljedeći: on može skočiti s jedne kutije na sljedeću u nizu ako je sljedeća kutija niža (nije bitno koliko) od one na kojoj se nalazi ili je najviše za  viša od one na kojoj se trenutno nalazi. Raspored kutija zovemo dobrim ako Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju, koristeći pritom samo dozvoljene skokove. Pitanje je sada: koliko postoji dobrih rasporeda?
viša od one na kojoj se trenutno nalazi. Raspored kutija zovemo dobrim ako Fiko može krenuti s prve kutije u nizu i skočiti redom na svaku iduću kutiju, koristeći pritom samo dozvoljene skokove. Pitanje je sada: koliko postoji dobrih rasporeda?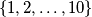 , pod uvjetom da kutije nazovemo redom brojevima
, pod uvjetom da kutije nazovemo redom brojevima  ,
,  ,
,  ,
,  . Dodatno, učinimo to na prirodan način: neka je kutija broj
. Dodatno, učinimo to na prirodan način: neka je kutija broj  visine
visine  , kutija broj
, kutija broj  visine
visine  , itd. do kutije broj
, itd. do kutije broj  . Permutacija inače nije ništa drugo doli uređeni (=,,u redu'') raspored nekih objekata.
. Permutacija inače nije ništa drugo doli uređeni (=,,u redu'') raspored nekih objekata.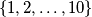 . Odgovor na ovo pitanje lijepo je objašnjen ovdje. Dakle, ukupno postoji
. Odgovor na ovo pitanje lijepo je objašnjen ovdje. Dakle, ukupno postoji 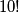 različitih permutacija, što je blago rečeno nezanemariv broj. Ovime smo ograničili broj dobrih permutacija na raspon
različitih permutacija, što je blago rečeno nezanemariv broj. Ovime smo ograničili broj dobrih permutacija na raspon  -
- 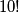 . Nije nešto, ali tek je početak. I barem smo uvjereni da ćemo ovaj zadatak teško riješiti ,,na prste''.
. Nije nešto, ali tek je početak. I barem smo uvjereni da ćemo ovaj zadatak teško riješiti ,,na prste''. kutije. Krećem i ja tim putem.
kutije. Krećem i ja tim putem. .
. , zadatak praktički ne postoji: jedina moguća permutacija je trivijalno dobra. Za
, zadatak praktički ne postoji: jedina moguća permutacija je trivijalno dobra. Za  , problem ostaje trivijalan, ali počinju bar neke kombinacije: obje moguće permutacije
, problem ostaje trivijalan, ali počinju bar neke kombinacije: obje moguće permutacije 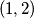 i
i 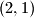 su dobre. Za
su dobre. Za 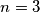 , od mogućih
, od mogućih  permutacija, vidim da
permutacija, vidim da  čine dobar raspored:
čine dobar raspored: 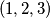 ,
, 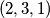 ,
, 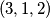 ,
, 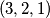 . Za
. Za 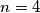 , već postoji
, već postoji 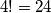 moguće permutacije. Od toga, sljedeće su dobre:
moguće permutacije. Od toga, sljedeće su dobre: 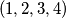 ,
, 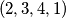 ,
, 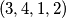 ,
,  ,
, 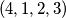 ,
, 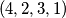 ,
, 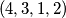 ,
, 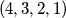 ; dakle
; dakle  ukupno. Uvjerite se sami da su napisani odgovori doista ispravni - nikad ne vjerujte slijepo autoru (pa ni meni)!
ukupno. Uvjerite se sami da su napisani odgovori doista ispravni - nikad ne vjerujte slijepo autoru (pa ni meni)! ,
,  ,
,  ,
,  -> nešto tu smrdi, i to na potencije broja
-> nešto tu smrdi, i to na potencije broja  ! Zašto, kako? Dobro, da se ne pravim lud previše, priznajem da sam između zadnjih redaka shvatio što se događa i došao do konačnog rješenja, kao možda i neki od vas. Idem sad probati opisati taj proces.
! Zašto, kako? Dobro, da se ne pravim lud previše, priznajem da sam između zadnjih redaka shvatio što se događa i došao do konačnog rješenja, kao možda i neki od vas. Idem sad probati opisati taj proces. i
i  . Prva opservacija je sljedeća: jedina novost između tri i četiri kutije je (očito) četvrta kutija visine
. Prva opservacija je sljedeća: jedina novost između tri i četiri kutije je (očito) četvrta kutija visine  . Prve tri kutije iz nekog dobrog rasporeda moraju ostati u istom međusobnom položaju kao i dok su bile samo tri, jer se dodavanjem četvrte ništa nije promijenilo ,,što se njih tiče''. Dakle, možemo početi od
. Prve tri kutije iz nekog dobrog rasporeda moraju ostati u istom međusobnom položaju kao i dok su bile samo tri, jer se dodavanjem četvrte ništa nije promijenilo ,,što se njih tiče''. Dakle, možemo početi od  dobra rasporeda koja imamo za slučaj s
dobra rasporeda koja imamo za slučaj s  kutije i pitati se gdje možemo ,,umetnuti" četvrtu kutiju.
kutije i pitati se gdje možemo ,,umetnuti" četvrtu kutiju.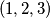 . Kutiju visine
. Kutiju visine  mogu staviti na početak, jer Fiko sa svojih
mogu staviti na početak, jer Fiko sa svojih  mačjih života može podnijeti skok prema dolje s bilo koje visine. Gdje još? Ne mogu iza
mačjih života može podnijeti skok prema dolje s bilo koje visine. Gdje još? Ne mogu iza  , to mu je previsoko. Isto tako i iza
, to mu je previsoko. Isto tako i iza  . Jedino može doći na kraj iza
. Jedino može doći na kraj iza  . Time od jednog dobrog rasporeda za
. Time od jednog dobrog rasporeda za 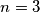 dobijem dva dobra rasporeda za
dobijem dva dobra rasporeda za 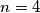 .
.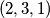 . Ponovno, kutiju
. Ponovno, kutiju  mogu staviti na početak, a osim toga opet jedino iza kutije
mogu staviti na početak, a osim toga opet jedino iza kutije  . Primjećujem da nakon što je umetnem tako između
. Primjećujem da nakon što je umetnem tako između  i
i  , nisam ništa ,,pokvario'', ponovno jer su dozvoljeni skokovi prema dolje s bilo koje visine. Dakle, i u ovom slučaju od jedne dobre permutacije za
, nisam ništa ,,pokvario'', ponovno jer su dozvoljeni skokovi prema dolje s bilo koje visine. Dakle, i u ovom slučaju od jedne dobre permutacije za 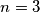 dobivam dvije dobre permutacije za
dobivam dvije dobre permutacije za 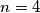 .
. za jedan. Plan je smišljen, pokušajmo ga provesti!
za jedan. Plan je smišljen, pokušajmo ga provesti!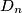 broj dobrih rasporeda s
broj dobrih rasporeda s  kutija. Želimo odrediti broj dobrih permutacija
kutija. Želimo odrediti broj dobrih permutacija 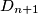 za
za  kutiju, u ovisnosti o
kutiju, u ovisnosti o 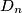 .
.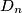 mogućih) za
mogućih) za  kutija. Označimo ga s
kutija. Označimo ga s 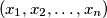 , gdje su jasno
, gdje su jasno  međusobno različiti elementi skupa
međusobno različiti elementi skupa 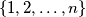 koji predstavljaju redni broj (ujedno i visinu) kutije. Sad se pitamo kako od ovog rasporeda možemo napraviti dobar raspored za
koji predstavljaju redni broj (ujedno i visinu) kutije. Sad se pitamo kako od ovog rasporeda možemo napraviti dobar raspored za  kutiju. Kao što smo prije zaključili, jedina stvar koju moramo napraviti je vidjeti gdje možemo ,,ubaciti'' kutiju
kutiju. Kao što smo prije zaključili, jedina stvar koju moramo napraviti je vidjeti gdje možemo ,,ubaciti'' kutiju  . Ponovno kao prije, vidimo da je sigurno možemo ubaciti na sami početak niza. Time dobivamo dobar raspored
. Ponovno kao prije, vidimo da je sigurno možemo ubaciti na sami početak niza. Time dobivamo dobar raspored 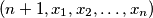 za
za  kutiju.
kutiju. . Sad neće biti na početku, što znači da će biti neka kutija ispred nje. To je ključ: da bi Fiko došao na kutiju
. Sad neće biti na početku, što znači da će biti neka kutija ispred nje. To je ključ: da bi Fiko došao na kutiju  dozvoljenim skokom, jedina mogućnost je da prije nje bude na kutiji
dozvoljenim skokom, jedina mogućnost je da prije nje bude na kutiji  , jer je to jedina manja s koje se može popeti na
, jer je to jedina manja s koje se može popeti na  , a više kutije od
, a više kutije od  nema. Dakle, ako je
nema. Dakle, ako je  takav da
takav da 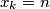 , još jedan dobar raspored za
, još jedan dobar raspored za  kutiju je
kutiju je 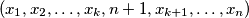 .
. kutija, dobivamo točno dva dobra rasporeda za
kutija, dobivamo točno dva dobra rasporeda za  kutiju. Možemo li zaključiti da vrijedi
kutiju. Možemo li zaključiti da vrijedi 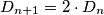 ? Skoro, ostaje dokazati da svi dobri rasporedi za
? Skoro, ostaje dokazati da svi dobri rasporedi za  kutiju moraju nastati upravo na ovaj način. Ali to nije teško i možda smo implicitno već dokazali u prijašnjoj raspravi, ostavljam vam za zadaću (HINT: uzme se proizvoljni raspored za
kutiju moraju nastati upravo na ovaj način. Ali to nije teško i možda smo implicitno već dokazali u prijašnjoj raspravi, ostavljam vam za zadaću (HINT: uzme se proizvoljni raspored za  kutiju i ,,izbriše'' se kutija
kutiju i ,,izbriše'' se kutija  : treba dokazati da je to dobar raspored za
: treba dokazati da je to dobar raspored za  kutija).
kutija).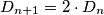 . Krasno! Ostaje riješiti ovu rekurziju. Rekurzije znaju biti zeznute, upravo zato što rekurzije znaju biti zeznute. Ali srećom, ova naša je ,,pitoma''. Početna vrijednost je
. Krasno! Ostaje riješiti ovu rekurziju. Rekurzije znaju biti zeznute, upravo zato što rekurzije znaju biti zeznute. Ali srećom, ova naša je ,,pitoma''. Početna vrijednost je 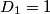 . Za
. Za 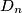 lako možemo razmotati:
lako možemo razmotati: 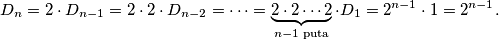
 , za sve
, za sve  (uklapa se čak i za polaznu vrijednost
(uklapa se čak i za polaznu vrijednost  ). Riješeno! Ostaje se vratiti na konkretno pitanje iz zadatka --- to ostavljam vama; kao rješenje prethodnog zadatka upišite dobivenu vrijednost.
). Riješeno! Ostaje se vratiti na konkretno pitanje iz zadatka --- to ostavljam vama; kao rješenje prethodnog zadatka upišite dobivenu vrijednost. ,
,  ,
,  ,
,  , nego nekih drugih? Što ako promijenimo Fikove sposobnosti skakanja uvis ili dolje? Ili još egzotičnije, što ako postoji više redova kutija, a ne samo jedan, pa pustimo Fika neka može skakati s reda na red? Što ako uključimo i Fikovu braću i sestre koji se isto žele igrati skakanja po kutijama? Samo je nebo granica i vaša mašta. Predlažem da svatko od vas smisli jednu varijantu Fikovog problema. Šaljite nam svoje zadatke i možda neke i uvrstimo u idući MetaMath!
, nego nekih drugih? Što ako promijenimo Fikove sposobnosti skakanja uvis ili dolje? Ili još egzotičnije, što ako postoji više redova kutija, a ne samo jedan, pa pustimo Fika neka može skakati s reda na red? Što ako uključimo i Fikovu braću i sestre koji se isto žele igrati skakanja po kutijama? Samo je nebo granica i vaša mašta. Predlažem da svatko od vas smisli jednu varijantu Fikovog problema. Šaljite nam svoje zadatke i možda neke i uvrstimo u idući MetaMath!