Nađite duljinu prostorne dijagonale kvadra sa poznatim duljinama bridova.
--------------------------------------------------------------------------------------------------
Rješenje.
1. Razumijevanje problema.
,,Što je nepoznato?'' Duljina prostorne dijagonale kvadra.
,,Što su poznati podatci?'' Duljine bridova kvadra.
,,Prikladno označimo veličine.'' Neka je  duljina prostorne dijagonale kvadra, a
duljina prostorne dijagonale kvadra, a  ,
,  i
i  duljine bridova.
duljine bridova.
,,Što povezuje  ,
,  ,
,  i
i  ?'' Sve su duljine dijelova kvadra -
?'' Sve su duljine dijelova kvadra -  ,
,  i
i  su duljine bridova, a
su duljine bridova, a  duljina prostorne dijagonale.
duljina prostorne dijagonale.
,,Jesu li zadani uvjeti dovoljni da se odredi nepoznato?'' Da. Budući da je kvadar određen bridovima duljina  ,
,  i
i  , prostorna dijagonala duljine
, prostorna dijagonala duljine  je također određena.
je također određena.
2. Smišljanje plana.
Ako se do sada rješavač nikad nije susreo sa zadatkom koji kao nepoznanicu ima prostornu dijagonalu kvadra, potrebno je razmisliti zna li se riješiti srodan, lakši zadatak. Kada su već u pitanju dijagonale, znamo li odrediti duljinu dijagonale pravokutnika ako su zadane duljine stranica? Da, koristeći Pitagorin poučak!
Budući da se koristio Pitagorin poučak, promatrali smo pravokutni trokut. Imamo li kakav pravokutni trokut negdje u našem zadatku?
Sada ne bi bilo loše nacrtati sliku.
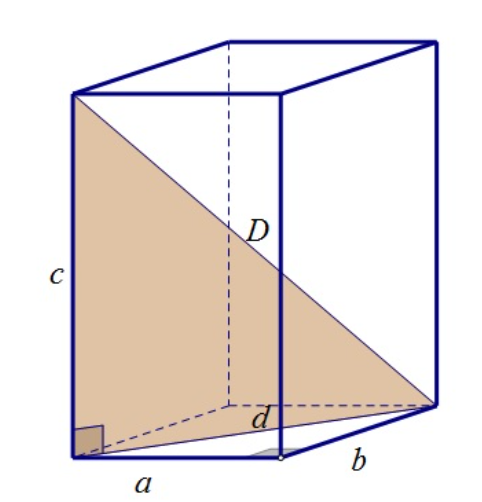
Uz uvođenje pomoćnog elementa, plošne dijagonale duljine  , uočavamo pravokutni trokut s katetama duljina
, uočavamo pravokutni trokut s katetama duljina  i
i  te duljine hipotenuze
te duljine hipotenuze  . Kada bismo znali odrediti
. Kada bismo znali odrediti  , tada bismo znali odrediti i
, tada bismo znali odrediti i  . No,
. No,  je duljina hipotenuze jednog drugog pravokutnog trokuta sa duljinama kateta
je duljina hipotenuze jednog drugog pravokutnog trokuta sa duljinama kateta  i
i  .
.
Imamo plan!
3. Provođenje plana.
Iz prvootkrivenog pravokutnog trokuta dobivamo: 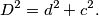 Iz drugog pravokutnog trokuta imamo:
Iz drugog pravokutnog trokuta imamo: 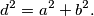 Uvrštavanjem umjesto
Uvrštavanjem umjesto 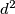 u prvu jednadžbu dobivamo
u prvu jednadžbu dobivamo 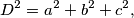 odnosno
odnosno 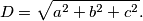 Svaki od koraka je jasan i ispravan.
Svaki od koraka je jasan i ispravan.
4. Osvrt.
,,Možemo li provjeriti rezultat?'' je u ovom slučaju pitanje na koje će neiskusnim rješavačima biti teško odgovoriti budući da je rješenje algebarske naravi, tj. ,,sa slovima.'' Jedna stvar koja je svakako istinita je da izraz za  sadrži poznate veličine
sadrži poznate veličine  ,
,  i
i  , dakle, iskoristili smo sve uvjete.
, dakle, iskoristili smo sve uvjete.
Ako bi smanjivanjem veličine  smanjivali visinu kvadra, u konačnici bi za
smanjivali visinu kvadra, u konačnici bi za 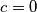 dobili pravokutnik sa stranicama duljina
dobili pravokutnik sa stranicama duljina  i
i  , a prostorna i plošna dijagonala bi se podudarale. Uvrštavanjem
, a prostorna i plošna dijagonala bi se podudarale. Uvrštavanjem 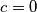 dobili bismo
dobili bismo 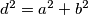 što je istinita tvrdnja za taj pravokutnik.
što je istinita tvrdnja za taj pravokutnik.
Istraživanjima (možda koristeći programe dinamičke geometrije) bismo mogli primijetiti da ako se  ,
,  i
i  produlje u istom omjeru, tada će se i prostorna dijagonala kvadra, nazovimo je
produlje u istom omjeru, tada će se i prostorna dijagonala kvadra, nazovimo je 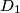 produljiti u tom omjeru. Npr. ako produljimo
produljiti u tom omjeru. Npr. ako produljimo  ,
,  i
i  2 puta, uvrštavanjem u formulu dobivamo:
2 puta, uvrštavanjem u formulu dobivamo: 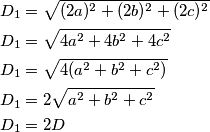 Time smo se uvjerili u tu tvrdnju. Nekim drugim uvrštavanjima bismo također mogli provjeriti valjanost formule.
Time smo se uvjerili u tu tvrdnju. Nekim drugim uvrštavanjima bismo također mogli provjeriti valjanost formule.
Kao rješenje upišite ,,Polya''.
Nađite duljinu prostorne dijagonale kvadra sa poznatim duljinama bridova.
--------------------------------------------------------------------------------------------------
\textit{Rješenje.}
\textbf{1. Razumijevanje problema.} \\\\
,,\textit{Što je nepoznato?}'' Duljina prostorne dijagonale kvadra. \\\\
,,\textit{Što su poznati podatci?}'' Duljine bridova kvadra. \\\\
,,\textit{Prikladno označimo veličine.}'' Neka je $D$ duljina prostorne dijagonale kvadra, a $a$, $b$ i $c$ duljine bridova. \\\\
,,\textit{Što povezuje $a$, $b$, $c$ i $D$?}'' Sve su duljine dijelova kvadra - $a$, $b$ i $c$ su duljine bridova, a $D$ duljina prostorne dijagonale. \\\\
,,\textit{Jesu li zadani uvjeti dovoljni da se odredi nepoznato?}'' Da. Budući da je kvadar određen bridovima duljina $a$, $b$ i $c$, prostorna dijagonala duljine $D$ je također određena.
\\\\
\textbf{2. Smišljanje plana.} \\\\
Ako se do sada rješavač nikad nije susreo sa zadatkom koji kao nepoznanicu ima prostornu dijagonalu kvadra, potrebno je razmisliti zna li se riješiti srodan, lakši zadatak. Kada su već u pitanju dijagonale, znamo li odrediti duljinu dijagonale pravokutnika ako su zadane duljine stranica? Da, koristeći Pitagorin poučak! \\\\
Budući da se koristio Pitagorin poučak, promatrali smo pravokutni trokut. Imamo li kakav pravokutni trokut negdje u našem zadatku? \\\\
Sada ne bi bilo loše nacrtati sliku. \\
\begin{center}
\includegraphics{kvadar.png}
\end{center}
Uz uvođenje pomoćnog elementa, plošne dijagonale duljine $d$, uočavamo pravokutni trokut s katetama duljina $c$ i $d$ te duljine hipotenuze $D$. Kada bismo znali odrediti $d$, tada bismo znali odrediti i $D$. No, $d$ je duljina hipotenuze jednog drugog pravokutnog trokuta sa duljinama kateta $a$ i $b$.
\\\\
Imamo plan!
\\\\
\textbf{3. Provođenje plana.} \\\\
Iz prvootkrivenog pravokutnog trokuta dobivamo:
$$
D^2=d^2+c^2.
$$
Iz drugog pravokutnog trokuta imamo:
$$
d^2=a^2+b^2.
$$
Uvrštavanjem umjesto $d^2$ u prvu jednadžbu dobivamo
$$
D^2=a^2+b^2+c^2,
$$
odnosno
$$
D=\sqrt{a^2+b^2+c^2}.
$$
Svaki od koraka je jasan i ispravan.
\\\\
\textbf{4. Osvrt.} \\\\
,,\textit{Možemo li provjeriti rezultat?}'' je u ovom slučaju pitanje na koje će neiskusnim rješavačima biti teško odgovoriti budući da je rješenje algebarske naravi, tj. ,,sa slovima.'' Jedna stvar koja je svakako istinita je da izraz za $D$ sadrži poznate veličine $a$, $b$ i $c$, dakle, iskoristili smo sve uvjete. \\\\
Ako bi smanjivanjem veličine $c$ smanjivali visinu kvadra, u konačnici bi za $c=0$ dobili pravokutnik sa stranicama duljina $a$ i $b$, a prostorna i plošna dijagonala bi se podudarale. Uvrštavanjem $c=0$ dobili bismo $d^2=a^2+b^2$ što je istinita tvrdnja za taj pravokutnik.
\\\\
Istraživanjima (možda koristeći programe dinamičke geometrije) bismo mogli primijetiti da ako se $a$, $b$ i $c$ produlje u istom omjeru, tada će se i prostorna dijagonala kvadra, nazovimo je $D_1$ produljiti u tom omjeru. Npr. ako produljimo $a$, $b$ i $c$ 2 puta, uvrštavanjem u formulu dobivamo:
\begin{align*}
D_1&=\sqrt{(2a)^2+(2b)^2+(2c)^2} \\
D_1&=\sqrt{4a^2+4b^2+4c^2} \\
D_1&=\sqrt{4(a^2+b^2+c^2)} \\
D_1&=2\sqrt{a^2+b^2+c^2} \\
D_1&=2D
\end{align*}
Time smo se uvjerili u tu tvrdnju. Nekim drugim uvrštavanjima bismo također mogli provjeriti valjanost formule.
\textit{Kao rješenje upišite ,,Polya''.}
 duljina prostorne dijagonale kvadra, a
duljina prostorne dijagonale kvadra, a  ,
,  i
i  duljine bridova.
duljine bridova.  ,
,  ,
,  i
i  ?'' Sve su duljine dijelova kvadra -
?'' Sve su duljine dijelova kvadra -  ,
,  i
i  su duljine bridova, a
su duljine bridova, a  duljina prostorne dijagonale.
duljina prostorne dijagonale.  ,
,  i
i  , prostorna dijagonala duljine
, prostorna dijagonala duljine  je također određena.
je također određena. 
 , uočavamo pravokutni trokut s katetama duljina
, uočavamo pravokutni trokut s katetama duljina  i
i  te duljine hipotenuze
te duljine hipotenuze  . Kada bismo znali odrediti
. Kada bismo znali odrediti  , tada bismo znali odrediti i
, tada bismo znali odrediti i  . No,
. No,  je duljina hipotenuze jednog drugog pravokutnog trokuta sa duljinama kateta
je duljina hipotenuze jednog drugog pravokutnog trokuta sa duljinama kateta  i
i  .
. 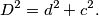 Iz drugog pravokutnog trokuta imamo:
Iz drugog pravokutnog trokuta imamo: 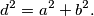 Uvrštavanjem umjesto
Uvrštavanjem umjesto 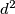 u prvu jednadžbu dobivamo
u prvu jednadžbu dobivamo 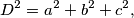 odnosno
odnosno 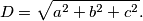 Svaki od koraka je jasan i ispravan.
Svaki od koraka je jasan i ispravan.  sadrži poznate veličine
sadrži poznate veličine  ,
,  i
i  , dakle, iskoristili smo sve uvjete.
, dakle, iskoristili smo sve uvjete.  smanjivali visinu kvadra, u konačnici bi za
smanjivali visinu kvadra, u konačnici bi za 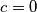 dobili pravokutnik sa stranicama duljina
dobili pravokutnik sa stranicama duljina  i
i  , a prostorna i plošna dijagonala bi se podudarale. Uvrštavanjem
, a prostorna i plošna dijagonala bi se podudarale. Uvrštavanjem 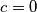 dobili bismo
dobili bismo 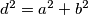 što je istinita tvrdnja za taj pravokutnik.
što je istinita tvrdnja za taj pravokutnik.  ,
,  i
i  produlje u istom omjeru, tada će se i prostorna dijagonala kvadra, nazovimo je
produlje u istom omjeru, tada će se i prostorna dijagonala kvadra, nazovimo je 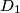 produljiti u tom omjeru. Npr. ako produljimo
produljiti u tom omjeru. Npr. ako produljimo  ,
,  i
i  2 puta, uvrštavanjem u formulu dobivamo:
2 puta, uvrštavanjem u formulu dobivamo: 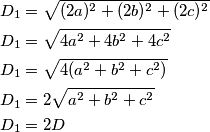 Time smo se uvjerili u tu tvrdnju. Nekim drugim uvrštavanjima bismo također mogli provjeriti valjanost formule.
Time smo se uvjerili u tu tvrdnju. Nekim drugim uvrštavanjima bismo također mogli provjeriti valjanost formule.