Dokazivanje 6
Zadatak 13. iz navedenog predavanja (nemojte se prepasti indukcije ako se niste susreli, možete razumjeti o čemu se radi i bez predznanja).
Uzmimo proizvoljan skup od konačno mnogo dužina u ravnini. Matematičkom indukcijom ćemo pokazati da sve dužine u tom skupu imaju jednaku duljinu.
Baza: u jednočlanom skupu trivijalno sve dužine imaju jednaku duljinu.
Pretpostavka: pretpostavimo da tvrdnja vrijedi za neki  , tj. da u svakom skupu od
, tj. da u svakom skupu od  dužina sve dužine imaju jednaku duljinu.
dužina sve dužine imaju jednaku duljinu.
Korak: uzmimo neki skup  od
od 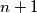 dužine. Izbacimo jednu dužinu iz
dužine. Izbacimo jednu dužinu iz  , nazovimo ju
, nazovimo ju  . Tako dobiveni skup
. Tako dobiveni skup 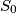 ima
ima  dužina, pa prema pretpostavci indukcije sve dužine u tom skupu imaju jednaku duljinu. Izbacivanjem neke dužine iz skupa
dužina, pa prema pretpostavci indukcije sve dužine u tom skupu imaju jednaku duljinu. Izbacivanjem neke dužine iz skupa 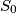 , dodavanjem dužine
, dodavanjem dužine  i ponovnom primjenom pretpostavke indukcije vidimo kako i dužina
i ponovnom primjenom pretpostavke indukcije vidimo kako i dužina  ima jednaku duljinu kao i sve ostale dužine iz skupa
ima jednaku duljinu kao i sve ostale dužine iz skupa 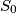 . Dakle, i sve dužine u skupu
. Dakle, i sve dužine u skupu  imaju jednaku duljinu.
imaju jednaku duljinu.
Ovime je korak indukcije dokazan, pa tvrdnja vrijedi za svaki  , tj. u svakom skupu od konačno mnogo dužina u ravnini, sve su dužine jednake duljine.
, tj. u svakom skupu od konačno mnogo dužina u ravnini, sve su dužine jednake duljine.
Gdje je greška u ovom dokazu?
