Dokažite sljedeće identitete: 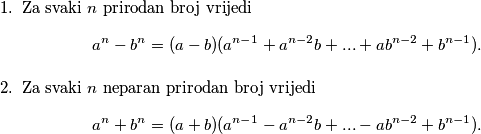
Rješenje.
Ovaj primjer tj. identiteti su bitniji od samog rješenje, budući da nemamo ništa pametnije napraviti nego pomnožiti desnu stranu i potvrditi da je jednaka lijevoj.
![\begin{enumerate}
\item
\begin{align*}
&(a-b)(a^{n-1}+a^{n-2}b+...+ab^{n-2}+b^{n-1}) =\\[8pt]
&=a^{n}+a^{n-1}b+a^{n-2}b^2+...+a^2b^{n-2}+ab^{n-1}+ \\
& \quad \quad -\Big(a^{n-1}b+a^{n-2}b^2+...+a^2b^{n-2}+ab^{n-1}+b^{n}\Big) \\[8pt]
&= a^n-b^n.
\end{align*}
Radi preglednosti smo pisali pomnožene zagrade u dva reda te malo pomaknuli kako bi lakše vidjeli jednake članove, prvi redak je $a$ pomnožen sa drugom zagradom, dok je drugi redak $-b$ pomnožen sa istom tom drugom zagradom.
\item
\begin{align*}
&(a+b)(a^{n-1}-a^{n-2}b+...-ab^{n-2}+b^{n-1}) =\\[8pt]
&=a^{n}-a^{n-1}b+a^{n-2}b^2-...-a^2b^{n-2}+ab^{n-1}+ \\
& \quad \quad \text{ }+a^{n-1}b-a^{n-2}b^2+...+a^2b^{n-2}-ab^{n-1}+b^{n} \\[8pt]
&= a^n+b^n.
\end{align*}
Primijetimo daje ključno da broj $n$ bude neparan, kako bi nam se poklopili predznaci te tako sve u sredini skratilo.
\end{enumerate}](/media/m/2/c/1/2c1592606e8d4ff3392aa149413aee93.png)
Kao rješenje upišite 1.
Dokažite sljedeće identitete:
\begin{enumerate}
\item Za svaki $n$ prirodan broj vrijedi
$$a^n-b^n = (a-b)(a^{n-1}+a^{n-2}b+...+ab^{n-2}+b^{n-1}).$$
\item Za svaki $n$ neparan prirodan broj vrijedi
$$a^n+b^n = (a+b)(a^{n-1}-a^{n-2}b+...-ab^{n-2}+b^{n-1}).$$
\end{enumerate}
\\
\textit{Rješenje.}
Ovaj primjer tj. identiteti su bitniji od samog rješenje, budući da nemamo ništa pametnije napraviti nego pomnožiti desnu stranu i potvrditi da je jednaka lijevoj.
\begin{enumerate}
\item
\begin{align*}
&(a-b)(a^{n-1}+a^{n-2}b+...+ab^{n-2}+b^{n-1}) =\\[8pt]
&=a^{n}+a^{n-1}b+a^{n-2}b^2+...+a^2b^{n-2}+ab^{n-1}+ \\
& \quad \quad -\Big(a^{n-1}b+a^{n-2}b^2+...+a^2b^{n-2}+ab^{n-1}+b^{n}\Big) \\[8pt]
&= a^n-b^n.
\end{align*}
Radi preglednosti smo pisali pomnožene zagrade u dva reda te malo pomaknuli kako bi lakše vidjeli jednake članove, prvi redak je $a$ pomnožen sa drugom zagradom, dok je drugi redak $-b$ pomnožen sa istom tom drugom zagradom.
\item
\begin{align*}
&(a+b)(a^{n-1}-a^{n-2}b+...-ab^{n-2}+b^{n-1}) =\\[8pt]
&=a^{n}-a^{n-1}b+a^{n-2}b^2-...-a^2b^{n-2}+ab^{n-1}+ \\
& \quad \quad \text{ }+a^{n-1}b-a^{n-2}b^2+...+a^2b^{n-2}-ab^{n-1}+b^{n} \\[8pt]
&= a^n+b^n.
\end{align*}
Primijetimo daje ključno da broj $n$ bude neparan, kako bi nam se poklopili predznaci te tako sve u sredini skratilo.
\end{enumerate}
\textit{Kao rješenje upišite 1.}