Izračunajte: 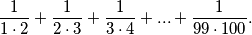
Rješenje.
Očito nećemo računati pješke sve razlomke tj. svoditi na zajedničke nazivnike, moramo nekako pametnije. Također nipošto nije poseban broj  , mogli bi računati izraz i do
, mogli bi računati izraz i do 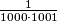 ili do općenito nekog
ili do općenito nekog 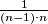 . Kad god to primijetimo i ne znamo kako pristupiti zadatku, nemamo nekih ideja, najbolje početi sa malim primjerima i nadati se uočavanju nekih pravilnosti, pa krenimo i mi tako.
. Kad god to primijetimo i ne znamo kako pristupiti zadatku, nemamo nekih ideja, najbolje početi sa malim primjerima i nadati se uočavanju nekih pravilnosti, pa krenimo i mi tako.
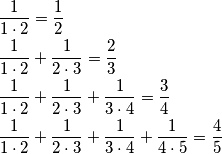 Doista postoji pravilnost, pretpostavljamo da će za općeniti slučaj biti
Doista postoji pravilnost, pretpostavljamo da će za općeniti slučaj biti 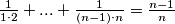 .
.
Sada se zadatak lako može riješiti matematičkom indukcijom, no mi ga ovdje nećemo tako. Koristit ćemo tehniku koja se, kasnijie će biti jasnije, zove teleskopiranje. Naime, željeli bi rastaviti svaki razlomak na više razlomaka (ovdje će biti samo dva) tako da se neki od njih u konačnici ponište (sa preostalima). Opći član u sumi izgleda 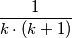 gdje je
gdje je  prirodan broj, te ukoliko bi ga htjeli rastaviti na neka dva razlomka, jedino smisleno bi bilo da ti razlomci imaju
prirodan broj, te ukoliko bi ga htjeli rastaviti na neka dva razlomka, jedino smisleno bi bilo da ti razlomci imaju  i
i  u nazivnicima no brojnike ćemo "namještati", probajmo naći koeficijente
u nazivnicima no brojnike ćemo "namještati", probajmo naći koeficijente 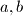 (ukoliko oni uopće postoje) takvi da
(ukoliko oni uopće postoje) takvi da 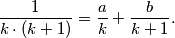 Svođenjem lijeve strane na zajednički nazivnik te množenjem obje strane sa
Svođenjem lijeve strane na zajednički nazivnik te množenjem obje strane sa 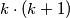 dobivamo
dobivamo 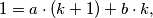 sada možemo grupirati koeficijente uz
sada možemo grupirati koeficijente uz  ,
, 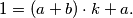 Kako želimo da ta jednakost vrijedi za svaki
Kako želimo da ta jednakost vrijedi za svaki  prirodan broj, možemo izjednačiti koeficijente (drugi način bi bio uvrstiti neke dvije vrijednosti u
prirodan broj, možemo izjednačiti koeficijente (drugi način bi bio uvrstiti neke dvije vrijednosti u  kako bi dobili dvije jednadžbe s dvije nepoznanice), kako na lijevoj strani nemamo ništa uz
kako bi dobili dvije jednadžbe s dvije nepoznanice), kako na lijevoj strani nemamo ništa uz  (imamo samo
(imamo samo  ) onda izjednačavanje izgleda ovako
) onda izjednačavanje izgleda ovako  ovaj sustav je lako riješiti te dobivamo jedinstveno rješenje (dakle postoji i jedino je takvo)
ovaj sustav je lako riješiti te dobivamo jedinstveno rješenje (dakle postoji i jedino je takvo)  , tj. naš rastav glasi
, tj. naš rastav glasi 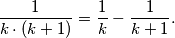
Sada možemo to iskoristiti na svakom razlomku početne sume kako bi dobili 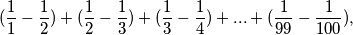 nakon poništavanja ostanu nam samo
nakon poništavanja ostanu nam samo 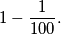 Za rješenje upišite 2.
Za rješenje upišite 2.
Izračunajte:
$$\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+...+\frac{1}{99\cdot 100}.$$
\textit{Rješenje.}
Očito nećemo računati pješke sve razlomke tj. svoditi na zajedničke nazivnike, moramo nekako pametnije. Također nipošto nije poseban broj $100$, mogli bi računati izraz i do $\frac{1}{1000\cdot 1001}$ ili do općenito nekog $\frac{1}{(n-1)\cdot n}$. Kad god to primijetimo i ne znamo kako pristupiti zadatku, nemamo nekih ideja, najbolje početi sa malim primjerima i nadati se uočavanju nekih pravilnosti, pa krenimo i mi tako.
\begin{align*}
&\frac{1}{1\cdot 2} = \frac{1}{2} \\
&\frac{1}{1\cdot 2} + \frac{1}{2\cdot 3} = \frac{2}{3} \\
&\frac{1}{1\cdot 2} + \frac{1}{2\cdot 3} + \frac{1}{3\cdot 4} = \frac{3}{4} \\
&\frac{1}{1\cdot 2} + \frac{1}{2\cdot 3} + \frac{1}{3\cdot 4} + \frac{1}{4\cdot 5} = \frac{4}{5} \\
\end{align*}
Doista postoji pravilnost, pretpostavljamo da će za općeniti slučaj biti $\frac{1}{1\cdot 2}+...+\frac{1}{(n-1)\cdot n} = \frac{n-1}{n}$.
Sada se zadatak lako može riješiti matematičkom indukcijom, no mi ga ovdje nećemo tako. Koristit ćemo tehniku koja se, kasnijie će biti jasnije, zove \textit{teleskopiranje}. Naime, željeli bi rastaviti svaki razlomak na više razlomaka (ovdje će biti samo dva) tako da se neki od njih u konačnici ponište (sa preostalima). Opći član u sumi izgleda
$$\frac{1}{k\cdot (k+1)}$$
gdje je $k$ prirodan broj, te ukoliko bi ga htjeli rastaviti na neka dva razlomka, jedino smisleno bi bilo da ti razlomci imaju $k$ i $k+1$ u nazivnicima no brojnike ćemo "namještati", probajmo naći koeficijente $a, b$ (ukoliko oni uopće postoje) takvi da
$$\frac{1}{k\cdot (k+1)} = \frac{a}{k}+\frac{b}{k+1}.$$
Svođenjem lijeve strane na zajednički nazivnik te množenjem obje strane sa $k\cdot(k+1)$ dobivamo
$$1 = a\cdot(k+1) + b\cdot k,$$
sada možemo grupirati koeficijente uz $k$,
$$1 = (a+b)\cdot k + a.$$
Kako želimo da ta jednakost vrijedi za svaki $k$ prirodan broj, možemo izjednačiti koeficijente (drugi način bi bio uvrstiti neke dvije vrijednosti u $k$ kako bi dobili dvije jednadžbe s dvije nepoznanice), kako na lijevoj strani nemamo ništa uz $k$ (imamo samo $1$) onda izjednačavanje izgleda ovako
\begin{align*}
0 &= a+b \\
1 &= a
\end{align*}
ovaj sustav je lako riješiti te dobivamo jedinstveno rješenje (dakle postoji i jedino je takvo) $a=1, b=-1$, tj. naš rastav glasi
$$\frac{1}{k\cdot (k+1)} = \frac{1}{k}-\frac{1}{k+1}.$$
Sada možemo to iskoristiti na svakom razlomku početne sume kako bi dobili
$$(\frac{1}{1}-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+...+(\frac{1}{99}-\frac{1}{100}),$$
nakon poništavanja ostanu nam samo
$$1-\frac{1}{100}.$$
\textit{Za rješenje upišite 2.}
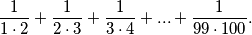
 , mogli bi računati izraz i do
, mogli bi računati izraz i do 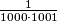 ili do općenito nekog
ili do općenito nekog 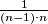 . Kad god to primijetimo i ne znamo kako pristupiti zadatku, nemamo nekih ideja, najbolje početi sa malim primjerima i nadati se uočavanju nekih pravilnosti, pa krenimo i mi tako.
. Kad god to primijetimo i ne znamo kako pristupiti zadatku, nemamo nekih ideja, najbolje početi sa malim primjerima i nadati se uočavanju nekih pravilnosti, pa krenimo i mi tako.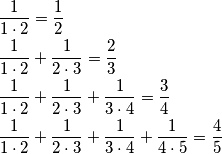 Doista postoji pravilnost, pretpostavljamo da će za općeniti slučaj biti
Doista postoji pravilnost, pretpostavljamo da će za općeniti slučaj biti 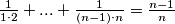 .
.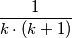 gdje je
gdje je  prirodan broj, te ukoliko bi ga htjeli rastaviti na neka dva razlomka, jedino smisleno bi bilo da ti razlomci imaju
prirodan broj, te ukoliko bi ga htjeli rastaviti na neka dva razlomka, jedino smisleno bi bilo da ti razlomci imaju  i
i  u nazivnicima no brojnike ćemo "namještati", probajmo naći koeficijente
u nazivnicima no brojnike ćemo "namještati", probajmo naći koeficijente 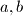 (ukoliko oni uopće postoje) takvi da
(ukoliko oni uopće postoje) takvi da 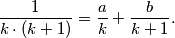 Svođenjem lijeve strane na zajednički nazivnik te množenjem obje strane sa
Svođenjem lijeve strane na zajednički nazivnik te množenjem obje strane sa 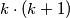 dobivamo
dobivamo 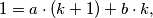 sada možemo grupirati koeficijente uz
sada možemo grupirati koeficijente uz  ,
, 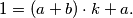 Kako želimo da ta jednakost vrijedi za svaki
Kako želimo da ta jednakost vrijedi za svaki  prirodan broj, možemo izjednačiti koeficijente (drugi način bi bio uvrstiti neke dvije vrijednosti u
prirodan broj, možemo izjednačiti koeficijente (drugi način bi bio uvrstiti neke dvije vrijednosti u  kako bi dobili dvije jednadžbe s dvije nepoznanice), kako na lijevoj strani nemamo ništa uz
kako bi dobili dvije jednadžbe s dvije nepoznanice), kako na lijevoj strani nemamo ništa uz  (imamo samo
(imamo samo  ) onda izjednačavanje izgleda ovako
) onda izjednačavanje izgleda ovako  ovaj sustav je lako riješiti te dobivamo jedinstveno rješenje (dakle postoji i jedino je takvo)
ovaj sustav je lako riješiti te dobivamo jedinstveno rješenje (dakle postoji i jedino je takvo)  , tj. naš rastav glasi
, tj. naš rastav glasi 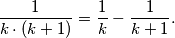
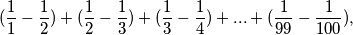 nakon poništavanja ostanu nam samo
nakon poništavanja ostanu nam samo 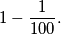 Za rješenje upišite 2.
Za rješenje upišite 2. 