Ako je 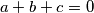 , dokaži da vrijedi
, dokaži da vrijedi 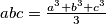 .
.
Rješenje.
Motivacija za prvi korak trebala bi biti jasna, u željenoj jednakosti postoje treće potencije a jedinu jednakost koju imamo 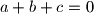 su samo prve, stoga ćemo sve potencirati na treću,
su samo prve, stoga ćemo sve potencirati na treću, 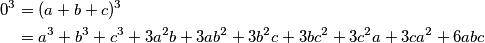 Sada možemo razmišljati obnuto, "unatrag", što nam je potrebno kako bismo dobili traženu jednakost?
Sada možemo razmišljati obnuto, "unatrag", što nam je potrebno kako bismo dobili traženu jednakost?
Na početku imamo željene treće potencije, dok na kraju umnožak  , no rastavimo li to na
, no rastavimo li to na 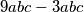 , potrebno je jedino na središnji dio bude jednak
, potrebno je jedino na središnji dio bude jednak  , tj.
, tj. 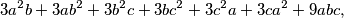 jer bi tada imali
jer bi tada imali 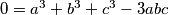 te bismo bili gotovi.
te bismo bili gotovi.
Ponovno, jedino šta nam je dano jest 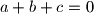 stoga bi bili jako sretni ukoliko bi mogli nekako faktorizirati izraz na taj faktor. Svi članovi imaju faktor
stoga bi bili jako sretni ukoliko bi mogli nekako faktorizirati izraz na taj faktor. Svi članovi imaju faktor  stoga možemo taj dio izlučiti te regrupirati
stoga možemo taj dio izlučiti te regrupirati ![\begin{align*}
3[a^2b+ab^2+b^2c&+bc^2+c^2a+ca^2+3abc] = \\
&=3[(a^2b+ab^2+abc)+(b^2c+bc^2+abc)+(c^2a+ca^2+abc)] = \\
&=3[ab(a+b+c)+bc(b+c+a)+ca(c+a+b)] = \\
&=3(a+b+c)[ab+bc+ca] = 0. \\
\end{align*}](/media/m/6/f/a/6fa891127290a887d177299daff57080.png)
Rješenje ovog primjera je 3.
Ako je $a+b+c = 0$, dokaži da vrijedi $abc = \frac{a^3+b^3+c^3}{3}$.
\textit{Rješenje.}
Motivacija za prvi korak trebala bi biti jasna, u željenoj jednakosti postoje treće potencije a jedinu jednakost koju imamo $a+b+c=0$ su samo prve, stoga ćemo sve potencirati na treću,
\begin{align*}
0^3 &= (a+b+c)^3 \\
&= a^3+b^3+c^3+3a^2b+3ab^2+3b^2c+3bc^2+3c^2a+3ca^2+6abc \\
\end{align*}
Sada možemo razmišljati obnuto, "unatrag", što nam je potrebno kako bismo dobili traženu jednakost?
Na početku imamo željene treće potencije, dok na kraju umnožak $6abc$, no rastavimo li to na $9abc-3abc$, potrebno je jedino na središnji dio bude jednak $0$, tj.
$$3a^2b+3ab^2+3b^2c+3bc^2+3c^2a+3ca^2+9abc,$$
jer bi tada imali $0 = a^3+b^3+c^3-3abc$ te bismo bili gotovi.
Ponovno, jedino šta nam je dano jest $a+b+c=0$ stoga bi bili jako sretni ukoliko bi mogli nekako faktorizirati izraz na taj faktor. Svi članovi imaju faktor $3$ stoga možemo taj dio izlučiti te regrupirati
\begin{align*}
3[a^2b+ab^2+b^2c&+bc^2+c^2a+ca^2+3abc] = \\
&=3[(a^2b+ab^2+abc)+(b^2c+bc^2+abc)+(c^2a+ca^2+abc)] = \\
&=3[ab(a+b+c)+bc(b+c+a)+ca(c+a+b)] = \\
&=3(a+b+c)[ab+bc+ca] = 0. \\
\end{align*}
\textit{Rješenje ovog primjera je 3.}
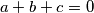 , dokaži da vrijedi
, dokaži da vrijedi 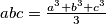 .
.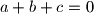 su samo prve, stoga ćemo sve potencirati na treću,
su samo prve, stoga ćemo sve potencirati na treću, 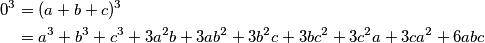 Sada možemo razmišljati obnuto, "unatrag", što nam je potrebno kako bismo dobili traženu jednakost?
Sada možemo razmišljati obnuto, "unatrag", što nam je potrebno kako bismo dobili traženu jednakost? , no rastavimo li to na
, no rastavimo li to na 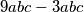 , potrebno je jedino na središnji dio bude jednak
, potrebno je jedino na središnji dio bude jednak  , tj.
, tj. 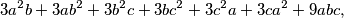 jer bi tada imali
jer bi tada imali 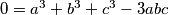 te bismo bili gotovi.
te bismo bili gotovi.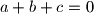 stoga bi bili jako sretni ukoliko bi mogli nekako faktorizirati izraz na taj faktor. Svi članovi imaju faktor
stoga bi bili jako sretni ukoliko bi mogli nekako faktorizirati izraz na taj faktor. Svi članovi imaju faktor  stoga možemo taj dio izlučiti te regrupirati
stoga možemo taj dio izlučiti te regrupirati ![\begin{align*}
3[a^2b+ab^2+b^2c&+bc^2+c^2a+ca^2+3abc] = \\
&=3[(a^2b+ab^2+abc)+(b^2c+bc^2+abc)+(c^2a+ca^2+abc)] = \\
&=3[ab(a+b+c)+bc(b+c+a)+ca(c+a+b)] = \\
&=3(a+b+c)[ab+bc+ca] = 0. \\
\end{align*}](/media/m/6/f/a/6fa891127290a887d177299daff57080.png)
