Nađite sva realna rješenja jednadžbe
$$\sqrt{2x-2\sqrt{2x-1}} - 2\sqrt{2x+3-4\sqrt{2x-1}} + 3\sqrt{2x+8-6\sqrt{2x-1}} = 4 \text{.}$$
\textit{Rješenje.}
Prvo ćemo uočiti da se izraz $2x-1$ podosta puta ponavlja te bi ga mogli supstituirat, neka je $y = 2x-1$, tada izraz napisan preko $y$ izgleda
$$\sqrt{y+1-2\sqrt{y}} - 2\sqrt{y+4-4\sqrt{y}} + 3\sqrt{y+9-6\sqrt{y}} = 4 \text{.}$$
Sada je lakše vidjeti kvadrate razlike ispod svakog korijena
$$\sqrt{(\sqrt{y}-1)^2} - 2\sqrt{(\sqrt{y}-2)^2} + 3\sqrt{(\sqrt{y}-3)^2} = 4 \text{.}$$
Ovo je odlično budući da možemo poništiti korijene i kvadrate, no treba biti i oprezan budući da ne znamo kakav je broj koji kvadriramo (negativan ili pozitivan) a kako svaki korijen je pozitivan tada moramo staviti apsolutne vrijednosti prilikom poništavanja, tj.
$$|\sqrt{y}-1|-2|\sqrt{y}-2|+3|\sqrt{y}-3| = 4.$$
Sada slijedi tehnički (samo računanje), ne tako lijep, dio zadatka u kojem svodimo na slučajeve,
\begin{enumerate}
\item $0\leq \sqrt{y} \leq 1$
$$1-\sqrt{y}-2(2-\sqrt{y})+3(3-\sqrt{y})=4$$
Nakon rješavanja dobivamo $\sqrt{y} = 1 \implies x=1.$
\item $1\leq \sqrt{y} \leq 2$
$$\sqrt{y}-1-2(2-\sqrt{y})+3(3-\sqrt{y})=4$$
Nakon rješavanja dobivamo $4=4$ što je istina uvijek, pa je rješenje ovog slučaja bilo koje (u tom intervalu) tj. cijeli interval $\sqrt{y} \in [1, 2] \implies x \in [1, \frac{5}{2}].$
\item $2\leq \sqrt{y} \leq 3$
$$\sqrt{y}-1-2(\sqrt{y}-2)+3(3-\sqrt{y})=4$$
Nakon rješavanja dobivamo $\sqrt{y} = 2 \implies x = \frac{5}{2}.$
\item $3\leq \sqrt{y}$
$$\sqrt{y}-1-2(\sqrt{y}-2)+3(\sqrt{y}-3)=4$$
Nakon rješavanja dobivamo $\sqrt{y} = 5 \implies x = 13.$
\end{enumerate}
Dakle, rješenja tražene jednadžbe su svi brojevi $x \in [1, \frac{5}{2}]\cup \{13\}$.
\textit{Kao rješenje upišite najveće rješenje zadane jednadžbe.}
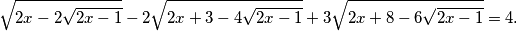
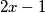 podosta puta ponavlja te bi ga mogli supstituirat, neka je
podosta puta ponavlja te bi ga mogli supstituirat, neka je 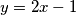 , tada izraz napisan preko
, tada izraz napisan preko  izgleda
izgleda 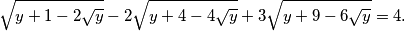 Sada je lakše vidjeti kvadrate razlike ispod svakog korijena
Sada je lakše vidjeti kvadrate razlike ispod svakog korijena 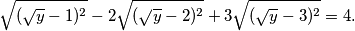 Ovo je odlično budući da možemo poništiti korijene i kvadrate, no treba biti i oprezan budući da ne znamo kakav je broj koji kvadriramo (negativan ili pozitivan) a kako svaki korijen je pozitivan tada moramo staviti apsolutne vrijednosti prilikom poništavanja, tj.
Ovo je odlično budući da možemo poništiti korijene i kvadrate, no treba biti i oprezan budući da ne znamo kakav je broj koji kvadriramo (negativan ili pozitivan) a kako svaki korijen je pozitivan tada moramo staviti apsolutne vrijednosti prilikom poništavanja, tj. 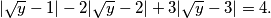
![\begin{enumerate}
\item $0\leq \sqrt{y} \leq 1$
$$1-\sqrt{y}-2(2-\sqrt{y})+3(3-\sqrt{y})=4$$
Nakon rješavanja dobivamo $\sqrt{y} = 1 \implies x=1.$
\item $1\leq \sqrt{y} \leq 2$
$$\sqrt{y}-1-2(2-\sqrt{y})+3(3-\sqrt{y})=4$$
Nakon rješavanja dobivamo $4=4$ što je istina uvijek, pa je rješenje ovog slučaja bilo koje (u tom intervalu) tj. cijeli interval $\sqrt{y} \in [1, 2] \implies x \in [1, \frac{5}{2}].$
\item $2\leq \sqrt{y} \leq 3$
$$\sqrt{y}-1-2(\sqrt{y}-2)+3(3-\sqrt{y})=4$$
Nakon rješavanja dobivamo $\sqrt{y} = 2 \implies x = \frac{5}{2}.$
\item $3\leq \sqrt{y}$
$$\sqrt{y}-1-2(\sqrt{y}-2)+3(\sqrt{y}-3)=4$$
Nakon rješavanja dobivamo $\sqrt{y} = 5 \implies x = 13.$
\end{enumerate}](/media/m/0/0/3/0038df7af8d727aeb12f7c2967b6f205.png) Dakle, rješenja tražene jednadžbe su svi brojevi
Dakle, rješenja tražene jednadžbe su svi brojevi ![x \in [1, \frac{5}{2}]\cup \{13\}](/media/m/4/7/7/477e32297278ae894ca4fb79461f6779.png) .
.