Diofantske - Primjer 1
Za prijevoz neke robe raspolažemo vrećama od 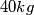 i
i 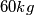 . Koje sve kombinacije vreća od
. Koje sve kombinacije vreća od 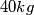 i
i 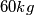 se mogu uzeti da bi se prenijelo
se mogu uzeti da bi se prenijelo 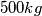 robe?
robe?
Rješenje:
Pokušajmo postaviti jednadžbu koja matematički objašnjava problem. Pretpostavimo da ćemo uzeti  vreća od po
vreća od po 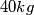 i
i  vreća od po
vreća od po 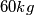 . Da bismo mogli robu prenijeti, potrebno je da vrijedi
. Da bismo mogli robu prenijeti, potrebno je da vrijedi 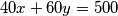 . Promatranjem ove jednadžbe, možemo pokratiti obje strane sa
. Promatranjem ove jednadžbe, možemo pokratiti obje strane sa  da dobijemo
da dobijemo 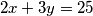 . Prebacivanjem
. Prebacivanjem 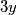 na desnu stranu i dijeljenjem sa
na desnu stranu i dijeljenjem sa  , dobijamo izraz za
, dobijamo izraz za  u zavisnosti od
u zavisnosti od  bez koeficijenta ispred
bez koeficijenta ispred  :
: 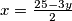 . Ovo je prirodan broj te zaključujemo da je neophodno uzeti neparan broj vreća od
. Ovo je prirodan broj te zaključujemo da je neophodno uzeti neparan broj vreća od 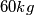 . Samim tim, shvaćamo da je ovo i dovoljan uvjet. Možemo uzeti
. Samim tim, shvaćamo da je ovo i dovoljan uvjet. Možemo uzeti 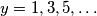 ovih vreća i da pri tome uzmemo odgovarajući broj
ovih vreća i da pri tome uzmemo odgovarajući broj 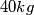 vreća takvih da uspijemo prenijeti robu. Uvedimo supstituciju
vreća takvih da uspijemo prenijeti robu. Uvedimo supstituciju 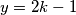 gdje je
gdje je  neki prirodan broj. Uvrštavanjem u
neki prirodan broj. Uvrštavanjem u 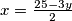 imamo da su sva rješenja ove jednadžbe opisana
imamo da su sva rješenja ove jednadžbe opisana 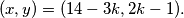 Sada trebamo paziti da je
Sada trebamo paziti da je  prirodan broj ili nula (nema smisla uzeti negativan broj vreća). Dakle, konačno sva rješenja su:
prirodan broj ili nula (nema smisla uzeti negativan broj vreća). Dakle, konačno sva rješenja su: 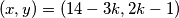 za svaki prirodan broj
za svaki prirodan broj  takav da
takav da 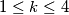 .
.
Za rješenje upišite 1
