Diofantske - Primjer 2
Riješiti diofantsku jednadžbu u skupu cijelih brojeva: 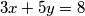
Rješenje:
Zapišimo jednadžbu na idući način: 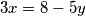 . Iz ovoga vidimo da kako
. Iz ovoga vidimo da kako  dijeli lijevu stranu, to
dijeli lijevu stranu, to  mora dijeliti i desnu stranu. S obzirom da
mora dijeliti i desnu stranu. S obzirom da  daje ostatak
daje ostatak  pri dijeljenju sa
pri dijeljenju sa  (odnosno
(odnosno  je kongruentno
je kongruentno  modulo
modulo  ) to znači da
) to znači da 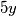 mora davati ostatak
mora davati ostatak  pri dijeljenju sa
pri dijeljenju sa  da bi desna strana bila djeljiva sa
da bi desna strana bila djeljiva sa  . S obzirom da
. S obzirom da  daje ostatak
daje ostatak  pri dijeljenju sa
pri dijeljenju sa  , to znači da
, to znači da  mora davati ostatak
mora davati ostatak  pri dijeljenju sa
pri dijeljenju sa  (provjerom ne može biti
(provjerom ne može biti  ili
ili  modulo
modulo  ). Zapišimo sada
). Zapišimo sada  u obliku
u obliku 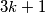 . Uvrštavanjem u zadanu jednadžbu i dijeljenjem obje strane sa
. Uvrštavanjem u zadanu jednadžbu i dijeljenjem obje strane sa  dobijamo
dobijamo 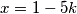 . Primijetimo da smo dobili jednoznačno određene
. Primijetimo da smo dobili jednoznačno određene 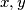 u funkciji od parametra
u funkciji od parametra  . Zaključujemo su rješenja zadane jednadžbe svi parovi oblika
. Zaključujemo su rješenja zadane jednadžbe svi parovi oblika 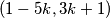 gdje je
gdje je  cijeli broj.
cijeli broj.
Uvjeriti se da ovakva procedura uvijek funkcionira i za opšti tip diofantske jednadžbe 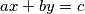 te izvesti njeno generalno rješenje. Kada sigurno nećemo imati rješenja ovakve jednadžbe?
te izvesti njeno generalno rješenje. Kada sigurno nećemo imati rješenja ovakve jednadžbe?
Za rješenje upišite 2
