MetaMath '23

Riješiti diofantsku jednadžbu 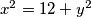$x^2 = 12+y^2$ u skupu cijelih brojeva. \textit{Rješenje:} Primijetimo da možemo prebaciti varijablu 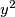$y^2$ lijevo i napraviti razliku kvadrata. Koristeći formulu za razliku kvadrata dobijamo 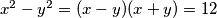$x^2-y^2 = (x-y)(x+y)=12$. Sada provjeravamo slučajeve kako se može dobiti $12$ kao umnožak dva cijela broja. Potrebno je promatrati slučajeve \[ (x-y,x+y) \in \{ (\pm 1, \pm 12),(\pm 12,\pm 1),(\pm 2,\pm 6),(\pm 6,\pm 2),(\pm 3,\pm 4),(\pm 4,\pm 3)\}. 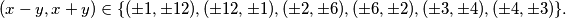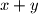\]Odbacujemo slučajeve gdje su $x-y$ i $x+y$ različite parnosti jer im je zbroj 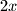$2x$ što je paran broj (ako bi bili različite parnosti, onda im zbroj mora biti neparan). Dakle preostaje provjeriti slučajeve 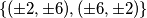$\{ (\pm 2,\pm 6),(\pm 6,\pm 2) \}$. Provjerimo slučajeve: 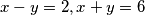$x-y=2, x+y=6$ slijedi zbrajanjem jednadžbi 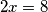$2x=8$ slijedi 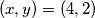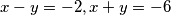$(x,y)=(4,2)$. $x-y=-2, x+y=-6$ dobijamo 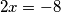$2x=-8$ odnosno 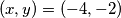$(x,y)=(-4,-2)$. Dakle, za minus slučajeve jasno uzmemo pozitivni slučaj i dodamo minus. Ostaje provjeriti još 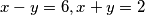$x-y=6, x+y=2$ odakle 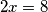$2x=8$ slijedi 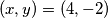$(x,y)=(4,-2)$ pa za negativni slučaj dobijamo 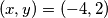$(x,y)=(-4,2)$. Dakle, sva rješenja su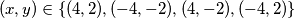 $(x,y) \in \{ (4,2),(-4,-2),(4,-2),(-4,2) \}$ \textit{Za rješenje upišite 4}