Diofantske - Primjer 3
Riješiti diofantsku jednadžbu u skupu prirodnih brojeva: 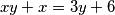
Rješenje:
Primijetimo da možemo izvući  sa lijeve strane i napisati jednadžbu na idući način:
sa lijeve strane i napisati jednadžbu na idući način: 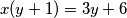 Sada možemo pokušati izvući
Sada možemo pokušati izvući  sa desne strane ali nas to neće dovesti daleko. Probajmo izvući
sa desne strane ali nas to neće dovesti daleko. Probajmo izvući  iz
iz  ali umjesto izvlačenja
ali umjesto izvlačenja  iz
iz  , napišimo
, napišimo  kao
kao 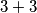 s ciljem pojavljivanja iste zagrade na desnoj kao i na lijevoj strani. Jednadžba postaje:
s ciljem pojavljivanja iste zagrade na desnoj kao i na lijevoj strani. Jednadžba postaje: 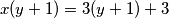 Prebacimo desnu zagradu lijevo i faktorizirajmo
Prebacimo desnu zagradu lijevo i faktorizirajmo 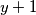 da dobijemo
da dobijemo 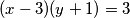 . Sada promotrimo lijevu stranu. Tu vidimo umnožak dva cijela broja. Na desnoj vidimo prosti broj
. Sada promotrimo lijevu stranu. Tu vidimo umnožak dva cijela broja. Na desnoj vidimo prosti broj  . Zaključujemo da zagrade na lijevoj strani čine permutaciju ili
. Zaključujemo da zagrade na lijevoj strani čine permutaciju ili 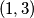 ili
ili 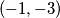 . Potrebno je ispitati sva četiri slučaja da bismo sa sigurnošću utvrdili točan skup rješenja ove jednadžbe. Probajmo riješiti jedan slučaj:
. Potrebno je ispitati sva četiri slučaja da bismo sa sigurnošću utvrdili točan skup rješenja ove jednadžbe. Probajmo riješiti jedan slučaj: 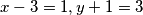 . Direktno dobijamo
. Direktno dobijamo 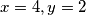 . Analognim zaključivanjem na preostala tri slučaja dobijamo rješenja:
. Analognim zaključivanjem na preostala tri slučaja dobijamo rješenja: 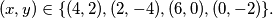
Da li se ovakvim postupkom mogu riješiti sve jednadžbe oblika 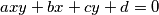 gdje su
gdje su 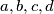 cijeli brojevi?
cijeli brojevi?
Za rješenje upišite 3.
